Kapitel 2. Allgemeine Grundbegriffe
2.1. Vorbemerkung
In dem Maße wie die Linguistik versucht eine exakte Wissenschaft zu sein,
erhalten Aussagen über ihre Gegenstände die Form von Theorien. Dabei müssen
grundsätzlich drei Aspekte unterschieden werden:
- Der Objektbereich, der durch eine Theorie erklärt oder durch ein Modell modelliert
werden soll. Dieser ist immer schon im Sinne eines Formalobjektes
(vgl. Kapitel 1.) zu verstehen.
- Die Theorie selbst, die den Objektbereich beschreibt und erklärt. Der gleiche
Objektbereich kann durch unterschiedliche Theorien erklärt werden.
- Die Sprache, in der eine Theorie ausgedrückt wird. Die gleiche Theorie kann
gegebenenfalls durch unterschiedliche Sprachen ausgedrückt werden. Ausdrücke
aus verschiedenen Sprachen sind dann ineinander übersetzbar.
Eine Theorie sollte zunächst in (gegebenenfalls terminologisch angereicherter)
Alltagssprache ausdrückbar sein. Es hat sich jedoch als vorteilhaft erwiesen,
in den Wissenschaften eine spezielle Wissenschaftssprache zu verwenden. Darüber
wird ausführlicher in Abschnitt 2.3. die
Rede sein.
2.2. Theorie und Theoriebildung
In den folgenden Abschnitten sollen zunächst kurz Begriffe wie
Theorie, Hypothese, theoretisches
Konstrukt erläutert werden.
Definition 2.1. Theorie
Eine Theorie ist ein System von Hypothesen oder eine Menge von solchen Systemen,
die zur Erklärung bestimmter Phänomenenbereiche entwickelt werden.
Definition 2.2. Hypothese
Eine Hypothese ist eine empirische Verallgemeinerung über einer Menge von Beobachtungsdaten.
Wir können zumindest vier Phasen der Theoriebildung unterscheiden.
- Sammlung und Beschreibung von empirischen Daten
- Hypothesenbildung
- Theoriebildung
- Überprüfung
PHASE 1
Beobachtungen über bestimmte Phänomene (Daten) werden gesammelt, beschrieben
und klassifiziert. So können wir z.B. beobachten, daß bestimmte Holzgegenstände
in Wasser schwimmen, während bestimmte (feste) Metallgegenstände untergehen.
Zum Zwecke der Beschreibung und Klassifizierung von Beobachtungsdaten werden Beschreibungssprachen
geschaffen (z.B. das phonetische Alphabet und die Terminologie der artikulatorischen
Phonetik). Das Resultat der Phase 1 ist eine Beschreibung und Klassifizierung einer
Menge von Beobachtungsdaten.
PHASE 2
Auf der Grundlage einer Sammlung von beschriebenen und klassifizierten Beobachtungsdaten
können wir versuchen Hypothesen zu bilden, wobei eine Hypothese eine empirische
Verallgemeinerung über die beobachteten Daten ist. Um bei unserem Beispiel
zu bleiben: Nachdem wir in einer großen Anzahl von Fällen festgestellt
haben, daß feste Holzgegenstände in Wasser schwimmen, während feste
Metallgegenstände untergehen, bilden wir die Hypothesen "Alle festen Holzgegenstände
schwimmen in Wasser" und "Alle festen Metallgegenstände gehen in
Wasser unter". Wir sehen jedoch noch keinen Zusammenhang zwischen diesen Hypothesen.
PHASE 3
Das grundlegende Ziel der Theoriebildung ist es, verschiedene Hypothesen durch allgemeine
Prinzipien miteinander in Beziehung zu setzen, und so eine Erklärung für
die gemachten Beobachtungen zu erhalten. Diese zur Erklärung herangezogenen
Prinzipien werden theoretische Konstrukte genannt. In unserem
Beispiel wird das unterschiedliche Verhalten von hölzernen und metallischen
Gegenständen durch das gleiche allgemeine Prinzip, das wir spezifisches Gewicht
nennen, erklärt. Das spezifische Gewicht ist die relative Dichte einer Substanz,
d.h. das Verhältnis der Dichte einer Substanz und der einer Vergleichssubstanz
(normalerweise Wasser).
Definition 2.3. Theoretisches Konstrukt
Ein theoretisches Konstrukt ist ein konstruierter, theoretischer oder theoriegebundener
Begriff, der nur indirekte empirische Bezüge hat. Systeme von Konstrukten
ergeben Theorien im Sinne begrifflicher Netze über einem Gegenstandsbereich.
Linguistische Konstrukte sind Struktur, System, Phonem, Kompetenz, usw.
Mit dem Begriff bzw. theoretischen Konstrukt des spezifischen Gewichtes können
nun die beiden Hypothesen
- Alle Holzgegenstände schwimmen in Wasser
- Alle festen Metallgegenstände gehen in Wasser unter
auf sehr allgemeine Weise miteinander in Beziehung gebracht werden:
Alle festen Körper, deren spezifisches Gewicht kleiner ist als das einer bestimmten
Flüssigkeit, schwimmen in dieser Flüssigkeit.
PHASE 4
Die Überprüfung von Theorien. Theorien werden überprüft, indem
man sie zu falsifizieren versucht. Der Wissenschaftler versucht Fälle zu finden,
die durch die Theorie nicht erklärt werden oder im Widerspruch zu den Vorhersagen
der Theorie stehen. Eine Theorie ist gültig solange sie nicht falsifiziert
worden ist. In unserem Beispiel kann die Hypothese, daß alle festen Metallgegenstände
in Wasser untergehen, durch die Beobachtung falsifiziert werden, daß Natrium
in Wasser schwimmt. Es handelt sich hier jedoch um eine Falsifizierung der ursprünglichen
Hypothese "alle Metallgegenstände gehen unter", aber nicht der Theorie.
Denn mit dem theoretischen Konstrukt des spezifischen Gewichts wird auch das Verhalten
von Natrium erklärt, dessen spezifisches Gewicht (0.97) kleiner als das von
Wasser (1.00) ist.
2.3. Wissenschaftssprache
Eine Theorie muß sprachlich ausgedrückt werden. Dies kann prinzipiell
mithilfe der Alltagssprache geschehen. Damit sind jedoch
eine Reihe von Schwierigkeiten verbunden, die dazu geführt haben, daß
zur Formulierung von wissenschaftlichen Theorien eine eigene Wissenschaftssprache
entwickelt worden ist.
Definition 2.4. Wissenschaftssprache
Die "Gesamtheit der sprachlichen Mittel einer Wissenschaft mit den Regeln für
deren Gebrauch" (Klaus/Buhr 1971, sv. Wissenschaftssprache) nennt man Wissenschaftssprache.
Die Grundlage einer Wissenschaftssprache ist immer die Alltagssprache. Gerade die
Eigenschaften der Alltagssprache, die ihre Flexibilität als Kommunikationsmittel
ausmachen, machen sie als Wissenschaftssprache jedoch ungeeignet: viele Wörter
der Alltagssprache sind mehrdeutig, ihre Bedeutung ist oft unscharf; die Alltagssprache
enthält Synonyme etc. Die Begriffe der Wissenschaftssprache müssen jedoch
eindeutig und genau sein. Die Wissenschaftssprache versucht diese Nachteile
der Alltagssprache zu überwinden, indem sie eine spezielle Terminologie verwendet,
die für die jeweilige Wissenschaft genau definierte Begriffe bezeichnet. Durch
eine solche Terminologie wird neben der Eindeutigkeit auch eine kürzere und
damit übersichtlichere Ausdrucksweise möglich.
Definition< 2.5. Theoretische Begriffe
Begriffe, die sich auf den von einer Theorie beschriebenen Gegenstand beziehen,
und die somit unmittelbare Bestandteil der Theorie sind, werden theoretische Begriffe
genannt.
Theoretische Begriffe der Sprachtheorie sind z.B.: Satz, Wort, Relativpronomen, Phonem
etc. Daneben sind auch Begriffe erforderlich, die Eigenschaften der Theorie selbst
erfassen, mit denen man also über Theorien spricht.
Definition 2.6. Metatheoretische Begriffe
Begriffe mit denen man über Eigenschaften von Theorien spricht werden metatheoretische
Begriffe genannt.
Metatheoretische Begriffe der Sprachtheorie sind z.B.: Transformationsregel, Strukturbeschreibung,
Regelschema, Symbolkette, grammatische Kategorie etc.
Die Wissenschaftssprache ist die Sprache, mit der eine Wissenschaft über ihre
Gegenstände spricht. Betrachten wir zunächst die Verwendung der Wissenschaftssprache
durch den Nicht-Linguisten.
Der Chemiker, z.B., verwendet Sprache um über Gegenstände zu sprechen,
die keine Sprache sind. Die Sprache, die er dazu verwendet, unterscheidet sich jedoch
von der Alltagssprache. Es ist eine besondere Sprache mit einem speziellen Vokabular,
einer Terminologie. Es ist ein Teil der Sprache, die wir Wissenschaftssprache genannt
haben. Nehmen wir folgendes Beispiel:
(2.1.) Natriumchlorid ist ein Salz
Natriumchlorid ist ein chemischer Terminus, den wir in der Alltagssprache
nicht verwenden. In einem Spezialwörterbuch würden wir als Bedeutung Salz
finden. Was passiert jedoch, wenn wir im Beispiel Natriumchlorid durch Salz
ersetzen?
(2.2.) Salz ist ein Salz.
Das ist etwas seltsam.
Für den Chemiker hat das Wort Salz eine besondere und allgemeinere Bedeutung.
(2.3.) Salz ist eine Substanz, die durch die Reaktion einer Säure
mit einer Base entsteht.
Noch genauer könnte diese Aussage wie folgt formuliert werden:
(2.4.) In der Chemie wird das Wort Salz zur Bezeichnung jeder
Substanz verwendet, die durch die Reaktion einer Säure mit einer Base entsteht.
Damit sollte deutlich geworden sein, daß auch der Nicht-Linguist Sprache in
zweierlei Funktionen verwendet. Er verwendet Sprache, um über Gegenstände
zu sprechen, die selbst nicht Sprache sind. Die Sprache, die er zu diesem Zweck
verwendet wird Objektsprache genannt.
Definition 2.7. Objektsprache
Der Teil der Wissenschaftssprache, mit der man über nicht-sprachliche Gegenstände
einer Wissenschaft spricht, wird Objektsprache genannt.
Der Wissenschaftler verwendet Sprache jedoch auch, um über Sprache zu sprechen,
z.B. über die Objektsprache seiner Wissenschaft. Das kann notwendig sein, um
z.B. die Bedeutung eines bestimmten Terminus zu definieren, wie im obigen Beispiel.
Definition 2.8. Metasprache
Jede Sprache mit der über eine Sprache gesprochen wird, ist eine Metasprache
Da eine Metasprache selbst wieder eine Sprache ist, kann man sich auch eine Metasprache
zu dieser Sprache vorstellen, eine Meta-Metasprache, so daß wir eine ganze
Hierarchie mit mehreren metasprachlichen Ebenen erhalten:
|
Metasprache der n-ten Stufe
|
|
∶
|
Metasprache der 2. Stufe
(Meta-Metasprache)
|
|
¯
|
|
Metasprache der 1. Stufe
|
|
¯
|
|
Objektsprache
|
|
¯
|
|
nichtsprachliche Objekte
|
Abb. 2.1. Objektsprache und Metasprachen
Eine Metasprache der ersten Stufe ist durch folgende Eigenschaften charakterisiert:
- Alles was in der Objektsprache ausgedrückt werden kann, kann auch in der zugeordneten
Metasprache ausgedrückt werden. Eine Metasprache muß so ausdrucksfähig
sein, daß sich alle Ausdrücke ihrer Objektsprache in sie übersetzen
lassen.
- Mittels der Metasprache kann man alle Ausdrücke der Objektsprache bezeichnen;
das bedeutet: Man hat Namen für sie (Namenmetasprache).
- Man kann in der Metasprache über alle Beschaffenheiten ihrer Objektsprache
sprechen.
- Man kann in der Metasprache Regeln für den Gebrauch der Objektsprache fomulieren.
Z.B. kann man den Gebrauch objektsprachlicher Termini durch Definitionen semantisch
regeln.
Für die Objektsprache gilt u.a. folgendes:
- Ist die Objektsprache eine wissenschaftliche Fachsprache, ist zumindest der Gebrauch
der Termini durch die zugehörige Metasprache semantisch geregelt.
- Die Objektsprache ist nicht selbst-rückbezüglich, d.h. in der Objektsprache
sind keine Aussagen über die Objektsprache selbst erlaubt.
Die Linguistik unterscheidet sich von anderen Wissenschaften u.a. darin, daß
ihr Objekt die Alltagssprache ist. Genau betrachtet hat die Linguistik daher keine
Objektsprache im definierten Sinn. Die Wissenschaftssprache der Linguistik ist daher
immer schon eine Metasprache. Wenn wir sagen: Peter hat zwei Silben, wollen
wir nicht über irgendeine Person sprechen, sondern über das Wort Peter.
Es handelt sich also um einen metasprachlichen Ausdruck. Das Wort Silbe bezeichnet
einen theoretischen Begriff und ist ebenfalls ein metasprachlicher Ausdruck.
Die Alltagssprache wird normalerweise verwendet um über nichtsprachliche Gegenstände
zu sprechen und fungiert dann als Objektsprache. Sie kann jedoch auch reflexiv verwendet
werden und fungiert dann als Metasprache. In der Alltagssprache kommen also sowohl
objektsprachliche als auch metasprachliche Ausdrücke vor. Der Ausdruck
Dieses Wort möchte ich nicht noch einmal hören ist sicher ein Ausdruck
der Alltagssprache. Gleichzeitig ist das Wort Wort ein metasprachlicher Ausdruck.
Um dieser besonderen Situation gerecht zu werden, soll der Begriff linguistischen
Objektsprache eingeführt werden:
Definition 2.9. Linguistische Objektsprache
In der Linguistik bezeichnet der Begriff Objektsprache eine natürliche Sprache
wenn sie selbst Gegenstand der Untersuchung ist. Die linguistische Objektsprache
ist reflexiv, d.h. sie kann metasprachliche Ausdrücke enthalten.
Angesichts der wichtigen Rolle, welche Sprache im menschlichen Leben spielt, ist
es keineswegs überraschend, daß die Alltagssprache eine Reihe von
Ausdrücken enthält, die sich auf sprachliche Gegenstände beziehen,
z.B. Satz, Wort, Laut, Buchstabe usw. Man vergleiche die folgenden Beispiele:
(2.5.) (a) Hans ist ein Narr
(b) Hans ist ein Nomen
(c) Hans ist einsilbig
(2.6.) (a) Sätze bestehen aus Wörtern
(b) Sätze besteht aus 5 Buchstaben
(2.7.) Was Hans zu dem Mann im Garten gesagt hat ist zweideutig.
Der Satz Hans ist ein Narr ist ein normaler objektsprachlicher Ausdruck,
mit dem eine Aussage über eine Person namens Hans gemacht wird. Der Satz Hans
ist ein Nomen hingegen macht nur Sinn, wenn Hans sich nicht auf irgendein
Individuum bezieht, sondern auf das Wort Hans selbst. Es handelt sich um
eine metalinguistische Aussage über das deutsche Wort Hans als Wort.
Man kann auch sagen, daß im ersten Fall das Wort Hans ‘gebraucht’
wird während es im zweiten Fall ‘erwähnt’ wird.
Wird ein Ausdruck erwähnt, fungiert er als Name für sich selbst.
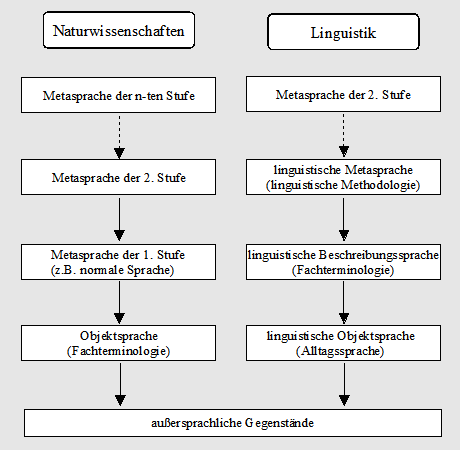
Abb. 2.2. Objekt- und Metasprache in Naturwissenschaft und Linguistik
Definition 2.10. Name
Ein Name ist ein metasprachlicher Ausdruck, der sich auf einen sprachlichen Ausdruck
bezieht, z.B. um darüber eine linguistische Aussage zu machen.
Der unterschiedliche Status von Hans in den beiden Sätzen kann durch
typographische Konventionen wie Anführungszeichen oder Kursivschrift verdeutlicht
werden:
(2.8.) Hans ist ein Nomen. Hans
ist ein Nomen.
Erwähnung kann rekursiv sein.
(2.9.) Das Subjekt von Hans
ist ein Nomen ist "Hans".
Vergleiche dazu auch folgendes Beispiel aus Carnap';s Buch The Logical Syntax
of Language (Carnap 1959: 156f.):
- ω ist eine Ordnungszahl;
ω
ist keine Ordnungszahl, sondern ein griechischer Buchstabe;
- Omega ist ein griechischer Buchstabe;
Omega
ist kein griechischer Buchstabe, sondern ein Wort, welches aus 5
Buchstaben besteht;
Im Satz (4) wird nicht über Omega gesprochen, also nicht über ω
,
sondern über Omega
. An Subjektstelle steht in (4) also nicht Omega
wie in Satz (3), sondern vielmehr "Omega".
Das Wort Nomen ist ebenfalls ein metalinguistischer Ausdruck. Es ist ein
Fachterminus, der einen theoretischen Begriff bezeichnet.
Definition 2.11. Linguistischer Terminus
Ein linguistischer Terminus ist ein metasprachlicher Ausdruck, dem ein linguistischer
Allgemeinbegriff durch Definition fest zugeordnet ist.
Der jeweilige begriffliche Inhalt linguistischer Termini muß möglichst
genau festgelegt werden. Dies kann durch Definitionen geschehen, durch welche die
einzelnen Begriffe voneinander abgegrenzt werden. Die einzelnen Begriffe erhalten
so einen festen Stellenwert im Rahmen eines zusammenhängenden Begriffssystems.
Definition 2.12. Definition
Unter einer Definition versteht man die genaue Abgrenzung eines Begriffes innerhalb
eines größeren Zusammenhanges unter Verwendung anderer Begriffe (explizite
Definition).
Definition 2.13. Definiendum
Der zu definierende Begriff heißt Definiendum (lat. das zu Definierende
).
Definition 2.14. Definiens
Der Begriff oder Begriffskomplex, durch den ein Begriff (das Definiendum) definiert
wird, heißt Definiens (lat. das, was definiert
).
Ein solches System besteht zunächst aus einer Reihe von Grundbegriffen, die
nicht explizit definiert werden können, sondern entweder durch ihre Stellung
im Gesamtsystem implizit definiert sind, oder im Rahmen einer anderen Theorie definiert
werden. Alle anderen Begriffe werden aus den Grundbegriffen durch Definition abgeleitet.
Dabei können verschiedene Arten von Definitionen unterschieden werden.
Definition 2.15. Realdefinition
Durch eine Realdefinition wird eine bereits bekannter
Begriff auf andere bekannte Ausdrücke in Übereinstimmung mit deren Bedeutungen
zurückgeführt (reduziert).
Definition 2.16. Nominaldefinition
Durch eine Nominaldefinition wird ein neuer Begriff in die Wissenschaftssprache
eingeführt und diese somit erweitert.
Ein typisches Beispiel für dieses Verfahren ist Bloomfields Artikel A
Set of Postulates...
(1926, vgl. Kapitel 1).
Dort wird beispielsweise Sprechakt als Grundbegriff vorausgesetzt und als Äusserung
bezeichnet:
Definition 2.17. Äußerung
Ein Sprechakt ist eine Äußerung.
Ein weiterer Grundbegriff ist gleich, der zusammen mit dem Terminus Äußerung
zur Definition von Sprachgemeinschaft herangezogen wird:
Definition 2.18. Sprachgemeinschaft
Innerhalb bestimmter Gemeinschaften sind aufeinander folgende Äußerungen
gleich oder teilweise gleich. Eine solche Gemeinschaft ist eine Sprachgemeinschaft
Nachdem nun auf diese Weise Äußerung und Sprachgemeinschaft definiert ist,
definiert Bloomfield Sprache wie folgt:
Definition 2.19. Sprache
Die Gesamtheit der Äußerungen, die in einer Sprachgemeinschaft gemacht
werden können, bildet die Sprache dieser Sprachgemeinschaft.
2.3.4. Beschreibungssprache
In 2.1.1 wurde Wissenschaftssprache definiert als die Gesamtheit der sprachlichen
Mittel einer Wissenschaft. Unter diesen Mitteln ist eine Teilmenge besonders wichtig,
nämlich die sprachlichen Mittel, mit denen die Theorien formuliert werden.
Dieser Teil einer Wissenchaftssprache soll Beschreibungssprache
genannt werden.
Wissenschaftliche Theorien sollen bestimmten Anforderungen genügen:
(a) Sie sollen widerspruchsfrei sein.
(b) Sie sollen adäquat sein, d.h. mit den Fakten übereinstimmen.
(c) Sie sollen explizit sein, d.h. sie sollen keine unausgesprochenen
Annahmen machen.
(d) Sie sollen einfach sein.
Die Anforderungen (b)–(d) können nicht unmittelbar, sondern nur im Vergleich
mit anderen Theorien überprüft werden. Ihre Überprüfung beruht
also auf Aussagen wie "die Theorie T1 ist einfacher (adäquater,
expliziter) als T2, weil ...".
Der Begriff widerspruchsfrei bezieht sich nicht direkt auf die beschriebenen
Sachverhalte, sondern auf den logischen Zusammenhang der Sätze der Theorie.
Es hat sich gezeigt, daß es leichter ist, Theorien zu entwickeln, die diesen
Anforderungen genügen, wenn man als Beschreibungssprache Kunstsprachen verwendet,
die nach bestimmten Prinzipien konstruiert sind: symbolisierte und formalisierte
Sprachen.
Definition 2.20. symbolisierte Sprache
Eine symbolisierte Sprache ist eine Sprache, "deren Zeichen (=Symbole) künstlich
geschaffen oder mit einer bestimmten neuen Bedeutung versehen wurden" (Klaus/Buhr
1971, sv. Sprache, symbolisierte).
Linguistische Symbole in diesem Sinne sind z.B. die Symbole für syntaktische
und lexikalische Kategorien wie z.B. S, NP, VP, AP, PP für Satz, Nominalphrase,
Verbalphrase, Adjektivphrase, Präpositionalphrase bzw. N, V, A, P
für Nomen, Verb, Adjektiv, Präposition. Die moderne Linguistik
bedient sich in vielen Bereichen einer symbolisierten Sprache. So kann z.B. die
Aussage "ein Satz (S) besteht aus (→) einer Nominalphrase (NP) verkettet
mit (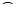
) einer Verbalphrase (VP)"
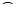durch den Ausdruck S → NPVP
symbolisiert werden. Eine symbolisierte Sprache muß in eine natürliche
Sprache übersetzbar sein, sonst ist sie sinnlos. Die Ausdrücke einer symbolisierten
Sprache sind wesentlich übersichtlicher und kürzer als deren Übersetzung
in die natürliche Sprache. Beispiel:
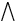x
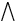y
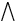z [S(z) ← z=x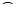y ∧ NP(x)
∧ VP(y)]
Die Übersetzung dieses Ausdrucks lautet: Für beliebige (Ketten) x, y, z
gilt: z ist ein Satz (S(z)), falls z gleich der Verkettung
von x und y ist (z=x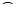y)
und x eine Nominalphrase (NP(x)) und y eine Verbalphrase (VP(y))
ist. Eine formalisierte Sprache ist meist eine symbolisierte Sprache im eben definierten
Sinne. Sie weist darüber hinaus eine Reihe weiterer Eigenschaften auf.
In einer formalisierten Sprache ist durch die Syntax genau festgelegt, welche Ausdrücke
in ihr möglich sind (wohlgeformt sind). Sie enthält Operationsregeln,
die es erlauben, aus wohlgeformten Ausdrücken neue wohlgeformte Ausdrücke
abzuleiten. Darüber hinaus ist durch eine Semantik festgelegt, wie die wohlgeformten
Ausdrücke zu interpretieren sind. Über formalisierte Sprachen verfügen
insbesondere Teilgebiete der formalen Logik und der Mathematik. Die Beschreibungssprache
der Linguistik ist primär eine symbolisierte Sprache. Es gibt jedoch auch in
der Linguistik Ansätze zu einer formalisierten Sprache. Voraussetzung
für den Aufbau einer formalisierten Sprache für ein bestimmtes Wissenschaftsgebiet
ist, daß dessen logische Struktur genau bekannt ist und formuliert werden
kann (vgl. Klaus/Buhr 1971, sv. Sprache, formalisierte). Das trifft für
die Linguistik jedoch nur in beschränktem Maße zu.
In seinem Buch Syntactic Structures definiert Chomsky Sprache wie folgt:
Definition 2.21. Sprache
Von nun an will ich Sprache als eine (endliche oder unendliche) Menge von Sätzen
auffassen, von welchen jeder von endlicher Länge und aus einer endlichen Menge
von Elementen aufgebaut ist. (Chomsky 1957: 13, Übers. K.H.W).
Diese Definition ist ganz allgemein und schließt natürliche Sprachen
nur als Sonderfall ein. Was für Objekte die Sätze einer Sprache tatsächlich
sind hängt davon ab, aus welchen Grundelementen sie aufgebaut sind.
Alle natürlichen Sprachen in ihrer gesprochenen und geschriebenen Form sind
Sprachen in diesem Sinne, da jede natürliche Sprache eine endliche Zahl von
Phonemen (oder Buchstaben des Alphabets) aufweist und jeder Satz als eine endliche
Folge dieser Phoneme (oder Buchstaben) darstellbar ist, obwohl es unbegrenzt viele
Sätze gibt. In ähnlicher Weise kann die Menge der Sätze
irgendeines formalisierten Systems der Mathematik als eine Sprache aufgefaßt
werden. (Chomsky 1957: 13, Übers. K.H.W.)
Insbesondere im Zusammenhang mit formalen Sprachen wird statt des Ausdrucks grammatisch
zur Charakterisierung der Sätze einer Sprache der Ausdruck wohlgeformt verwendet.
Ungrammatische
Ausdrücke sind nicht wohlgeformt.
Gegeben sei beispielsweise folgende formale Sprache: L = {ab, aabb, aaabbb …}
Die folgenden Ketten sind nicht wohlgeformt:
*ba, *aab, *abb, *aba, *ababbb.
Die allgemeine Form eines Satzes in L ist also anbn,
d.h. eine Folge von n a
gefolgt von einer Folge von n b
.
Unter der Annahme, daß es für n keine Obergrenze gibt, können
die Sätze
in L nicht einfach durch Aufzählung definiert
werden. Es ist also ein (endliches) Verfahren notwendig, das bestimmt welche der
theoretisch möglichen Folgen von a und b in L enthalten
sind. Die folgenden Regeln reichen dafür aus:
(a) ab ist in L
(b) Wenn S in L ist, dann ist auch aSb in L
(c) Nur nach (1) und (2) zulässige Ausdrücke sind in
L.
Dabei steht das Symbol S für eine beliebige bereits als Satz von L
identifizierte Folge von a und b.
|
Ableitungsbeispiel:
|
(1) ab
|
Regel 1
|
|
(2) aabb
|
Regel 2, (1)
|
|
(3) aaabbb
|
Regel 2, (2)
|
|
(4) aaaabbbb
|
Regel 2, (3)
|
Im obigen Zitat aus Chomsky (1957) wird der Ausdruck formalisiertes System
verwendet. Ein formalisiertes System (formales System) ist ein Symbolsystem, in
dem dafür definierte Operationen mechanisch ausgeführt werden können,
ohne daß man wissen muß, wofür die Symbole in Wirklichkeit stehen.
Formalisierte Systeme werden durch Sprachen im oben definierten Sinne ausgedrückt.
Ein anderer Ausdruck für eine formale Sprache ist Kalkül.
Definition 2.22. Kalkül
Die Sprache eines formalisierten Systems wird Kalkül genannt.
Definition 2.23. uninterpretiertes Kalkül
Ein Kalkül, dessen Formationsregeln oder syntaktische Regeln, festgelegt sind,
für dessen Ausdrücke aber noch keine Interpretation geliefert worden ist,
ist ein uninterpretiertes Kalkül.
Definition 2.24. interpretiertes Kalkül
Ein Kalkül, für das sowohl syntaktische als auch semantische Regeln gegeben
sind, ist ein interpretiertes Kalkül.
Definition 2.25. formalisierte Sprache
Eine formalisierte Sprache ist ein interpretiertes Kalkül.
Es gibt formalisierte Systeme, die mehrere verschiedene konkrete Interpretationen
haben. Ein Beispiel dafür ist etwa die Boolesche Algebra, die als Kalkülisierung
sowohl der Mengentheorie als auch der Aussagenlogik verstanden werden kann.
Im folgenden Kapitel werden wir uns ausführlich mit der Aussagenlogik im Sinne
einer formalisierten Sprache, d.h. eines interpretierten Kalküls befassen.
2.3 Literatur
Bloomfield, Leonard
1926 A Set of Postulates for the Science of
Language. In: Language 2, 153–4.
Carnap, Rudolf
1959 The Logical Syntax of Language.
Transl. by Amethe Smeaton, Littlefield, Adams & Co.: Paterson, N.J.
Chomsky, Noam
1957 Syntactic Structures. Mouton:
The Hague
Esser, Wilhelm K.
1970 Wissenschaftstheorie I. Definition und Reduktion.
Alber: Freiburg/München.
Klaus, Georg und Manfred Buhr (Hg.)
1971 Philosophisches Wörterbuch. Berlin: das europäische buch.
Suppes, Patrick
1957 Introduction to Logic. D. van Nostrand
Company, Inc.: Princeton, N.J./
Toronto/ London/New York.
von Savigny, Eike
1970 Grundkurs im wissenschaftlichen Definieren.
Übungen zum Selbststudium. dtv: München.