Kapitel 4. Grundbegriffe der Prädikatenlogik

Wir haben gesehen, daß eine der wesentlichen Aufgaben der Aussagenlogik die Untersuchung des logischen Schließens ist. Es ging u.a. darum zu zeigen, unter welchen allgemeinen Bedingungen Schlüsse gültig sind. Es ist gezeigt worden, daß ein Schluß dann gültig ist, wenn er die Instanz (ein Einsetzungsbeispiel) eines gültigen Schlußschemas ist, wobei die Gültigkeit eines Schlußschemas auschließlich eine Folge des formalen Aufbaus des Schemas ist. Beispielsweise ist der Schluß

(4.1.)  Wenn Sokrates ein Mensch ist, dann ist er sterblich
Sokrates ist ein Mensch
Sokrates ist sterblich

eine Instanz des gültigen Schlußschemas (ModusPonens)

(4.2.)  q
p
∴ q

Dabei sind p und q Aussagenvariable, die für beliebige Aussagen stehen, deren innerer Aufbau ohne Belang ist. Aus der Nichtberücksichtigung der inneren Struktur von Aussagen ergeben sich allerdings Probleme. Man wird beispielsweise sagen wollen, daß auch der folgende Schluß gültig ist:

(4.3.)  Menschen sind sterblich
Sokrates ist ein Mensch
∴ Sokrates ist sterblich

Diese intuitive Einsicht läßt sich jedoch im Rahmen der Aussagenlogik nicht mehr begründen. Wenn wir die Aussagen dieses Schlusses durch Variable ersetzen erhalten wir folgendes Schema

(4.4.)  p
q
∴r

Dies ist keinesfalls ein gültiges Schema, denn die Aussagenform p ∧ q ⇒ r ist keine Tautologie.

Man betrachte weiterhin die folgenden Beispiele:

(4.5.)  Manche Menschen sind faul.
Alle Faulen schlafen viel
∴Manche Menschen schlafen viel
(4.6.)  Ein Pferd ist ein Tier
∴ Ein Pferdekopf ist der Kopf eines Tieres
(4.7.)  Hans ist ein Junggeselle
Alle männlichen Verwandten von Maria sind verheiratet
∴ Hans ist nicht der Onkel von Maria

Es handelt sich in allen drei Fällen um gültige Schlüsse. Die Frage jedoch, inwieweit die Gültigkeit dieser Schlüsse allein von der Form abhängt, kann nicht mehr im Rahmen der Aussagenlogik geklärt werden. Dazu muß vielmehr die innere Struktur der Aussagen selbst mit berücksichtigt werden. Dafür sind zusätzliche sprachliche Ausdrucksmittel erforderlich, die in der Prädikatenlogik entwickelt werden. Die Prädikatenlogik ist also eine Erweiterung der Aussagenlogik.[1]

Sie untersucht ebenfalls Aussagen und Aussagenverbindungen. Während die Aussagenlogik aber die Aussagen als unanalysierte Ganzheiten betrachtet, untersucht die Prädikatenlogik auch die innere Struktur von Aussagen.

4.1. Individuen und Prädikate

Für die Prädikatenlogik sind Aussagen selbst komplexe Gebilde, die nach bestimmten Regeln aufgebaut sind. Eine genauere Darstellung der Syntax der Prädikatenlogik folgt später. Wir wollen zunächst informell von der Annahme ausgehen, daß Aussagen aus Begriffen zusammengesetzt sind. Man vergleiche die folgenden Sätze:

(4.8.) Der Mond ist ein Planet

(4.9.) Das Pferd ist ein Säugetier

Beide Sätze sind Ausdrücke für Aussagen. Sie haben die gleiche syntaktische Struktur. Für die Aussagenlogik entscheidend ist nur, daß (4.8) eine falsche Aussage ist, (4.9) dagegen eine wahre. Untersucht man jedoch die logische Struktur dieser Aussagen genauer, so zeigt sich, daß sie sich in wesentlichen Punkten unterscheiden.

Das Wort Mond bezeichnet in der Alltagssprache einen Individualbegriff, d.h. einen Begriff, der ein einziges Individuum repräsentiert. Es ist also ein Name wie die Eigennamen Peter, Fritz, etc. Namen als Zeichen für Individualbegriffe werden in der Prädikatenlogik Individuenkonstanten genannt und konventionell durch die ersten Buchstaben des Alphabets (a, b, c …) symbolisiert.

Die Wörter Planet, Pferd und Säugetier bezeichnen dagegen Allgemeinbegriffe, d.h. Begriffe, die eine Klasse repräsentieren und damit auf alle Elemente dieser Klasse zutreffen.

Der Satz Der Mond ist ein Planet sagt aus, daß dem Individuum Mond das Prädikat Planet zukommt. Man schreibt dafür

(4.10.) Planet(Mond)

Ein Prädikat kann ein Zeichen für einen Allgemeinbegriff sein (z.B. Planet, Pferd, Säugetier), aber auch ein Zeichen für einen Eigenschaftsbegriff (z.B. groß, klein, rot). Der Satz (4.11)(a) hat also die gleiche logische Struktur wie der Satz (4.11)(b):

(4.11.)  (a) Peter ist Student
(b) Peter ist dumm 		Student (Peter)
dumm(Peter)

Der prädikatenlogische Begriff 'Prädikat' darf also nicht mit dem grammatischen Begriff der traditionellen Grammatik verwechselt werden.

4.2. Quantoren

4.2.1. Allquantor

Nicht alle Aussagen enthalten Individualbegriffe. Das zeigt die Analyse des Satzes

(4.9) Das Pferd ist ein Säugetier

Man kann statt dessen auch sagen

(4.12.)  (a) Ein Pferd ist ein Säugetier oder
(b) Pferde sind Säugetiere

Die Bedeutung dieser Aussage läßt sich etwa wie folgt umschreiben

(4.13.) Wenn etwas ein Pferd ist, dann ist es auch ein Säugetier.

Dabei sind etwas und es die umgangssprachliche Wiedergabe von Variablen, die für beliebige Individuen eines Individuenbereichs stehen. Die Ausdrücke etwas ist ein Pferd bzw. es ist ein Säugetier werden wie folgt symbolisiert

(4.14.)  (a) Pferd(x)
(b) Säugetier(x)

Solche Ausdrücke bezeichnet man als Aussagenformen. Dabei ist x eine Leerstelle, in die eine Individuenkonstante (z.B. Halla) eingesetzt werden kann. Man nennt solche Leerstellen Individuenvariablen.

Definition 4.1. Aussageform

Eine Aussageform ist ein Ausdruck, der bei Ersetzung der Individuenvariablen durch Individuenkonstanten in eine Aussage übergeht.

Die Formulierung (4.13) zeigt, daß in (4.9) sozusagen die folgende Implikation steckt:

(4.15.) Pferd(x) ⇒ Säugetier(x)

Das ist noch keine Aussage, sondern ebenfalls eine Aussageform. Sie wird zu einer Aussage dadurch, daß die Individuenvariable durch eine Individuenkonstante ersetzt wird, z.B.:

(4.16.)  (a) Pferd(Halla) ⇒ Säugetier(Halla)
(b) Pferd(Nimrod) ⇒ Säugetier(Nimrod)

Die Aussagenform (4.15) wird zu einer Aussage auch durch den Zusatz, daß sie für jedes beliebige x gelten soll. Das kommt auch durch die folgenden Paraphrasen von (4.9.) zum Ausdruck:

(4.17.)  (a) Jedes Pferd ist ein Säugetier
(b) Alle Pferde sind Säugetiere

Dafür kann man formeller sagen:

(4.18.) Für alle (jedes) x gilt: wenn x ein Pferd ist, dann ist x auch ein Säugetier

Der Ausdruck für alle (jedes) x gilt wird durch x symbolisiert. Der Ausdruck x wird Allquantor genannt.[2]

Dieses Zeichen kann als ein großes Konjunktionszeichen aufgefaßt werden, denn der Allquantor kann als "Summierung" einer Konjunktion von Elementaraussagen aufgefaßt werden:

x=an

x p(x) = p(a1) ∧ p(a2) ∧…∧ p(an).

x=a1

Eine Aussageform wie (4.9.) wird zu einer Aussage, wenn man sie durch einen Quantor “bindet”. Dabei wird der Quantor vor die Aussageform gestellt, auf die er sich bezieht:

(4.19.)  x (Pferd(x) ⇒ Säugetier( x))

Der Ausdruck (4.19.) ist die prädikatenlogische Darstellung der Aussage (4.9.)

Die Analyse hat gezeigt, daß die äußerlich so ähnlichen Sätze (4.8.) und (4.9.) Aussagen von sehr verschiedener Struktur ausdrücken.

Die Analyse der internen Struktur von Aussagen ist notwendig, um die Gesetzmäßigkeiten des logischen Schließens untersuchen zu können. Wir haben eingangs gesagt, daß die Gültigkeit des Schlusses (4.3.) mit den Mitteln der Aussagenlogik nicht zu etablieren ist. Die gleiche Struktur hat

(4.20.) Fußballspieler sind bestechlich
Fritz ist ein Fußballspieler
Fritz ist bestechlich

In prädikatenlogischer Darstellung lautet dieser Schluß:

(4.21.) (a) x (Fußballspieler(x) ⇒  bestechlich(x))
(b) Fußballspieler(Fritz)
(c)∴bestechlich(Fritz)

Aussagen mit einem Allquantor werden Allaussagen genannt. Sie sollen für alle Objekte eines bestimmten Gegenstandsbereichs gelten. Allaussagen gehen in Einzelaussagen über, wenn man die Variablen durch Konstanten ersetzt.

Ersetzt man in (4.21.) (a) die Variable durch Fritz, so erhält man die Einzelaussage

(4.22.) Fußballspieler(Fritz) ⇒ bestechlich (Fritz)

Die Allaussage (4.21.)(a) wird als wahr vorausgesetzt. Folglich muß auch die Aussage (4.22.)als wahr vorausgesetzt werden, denn sie ist nur ein Sonderfall von (4.21.)(a). Es gilt allgemein das folgende Schlußschema (Allbeseitigung):

(4.23.)  x p(x)
∴ p(a)

Damit läßt sich der Schluß (4.21.)(a) zurückführen auf das Schema Modus Ponens:

(4.24.)

(1)  x  (Fußballspieler(x) ⇒ bestechlich( x)) Prämisse
(2)  Fußballspieler(Fritz) Prämisse
(3)  Fußballspieler(Fritz) ⇒ bestechlich(Fritz) (1) Allbeseitigung
(4)  bestechlich(Fritz) (2), (3), Modus Ponens

4.2.2. Existenzquantor

Neben Allaussagen gibt es noch andere “quantifizierte” Aussagen, z.B.:

(4.25.) Einige Menschen sind Kannibalen

Wenn jemand (4.25.) behauptet, dann kann er den Beweis für seine Behauptung antreten, indem er mindestens einen Menschen vorführt, auf den das Prädikat Kannibale zutrifft. Wenn es mehr als einer ist, umso besser. Der logische Sinn von (4.25.) ist also:

(4.26.) Es gibt mindestens einen Menschen, der Kannibale ist

(4.27.) Es gibt mindestens ein x, für das gilt: x ist ein Mensch und x ist Kannibale.

Der Ausdruck es gibt (mindestens) ein x, für das gilt wird durch das Zeichen x symbolisiert und Existenzquantor genannt. Aussagen mit Existenzquantor heißen Existenzaussagen, sie behaupten die Existenz von Objekten mit bestimmten Eigenschaften.[3]

Das Zeichen ist ein großes Disjunktionszeichen, was darin begründet ist, daß eine Existenzaussage als die "Summierung" einer Disjunktion von Elementaraussagen aufgefaßt werden kann:

x = an

p(x) = p(a 1) ∨ p(a2) ∨ … ∨  p(an)

x = a1

Die prädikatenlogische Darstellung von (4.25.) lautet also:

(4.28.)   x (Mensch(x) ∧ Kannibale(x))

4.2.3. Das Verhältnis von Allquantor und Existenzquantor

Wie muß nun ein Satz wie (4.29.) prädikatenlogisch dargestellt werden?

(4.29.) Kein Mensch ist unfehlbar

Es wird offenbar ausgesagt, daß das Prädikat unfehlbar auf keinen Menschen zutrifft, anders ausgedrückt, daß für alle Menschen gilt, daß sie nicht unfehlbar sind:

(4.30.)  (a) Für alle x gilt: wenn x ein Mensch ist, dann ist es nicht der Fall, daß x unfehlbar ist.
(b) x (Mensch(x) ⇒ ¬unfehlbar( x))

Genausogut hätte man allerdings auch formulieren können

(4.31.)  (a) Für alle x gilt: es ist nicht der Fall, daß x ein Mensch und gleichzeitig unfehlbar ist.
(b) x ¬(Mensch(x) ∧ unfehlbar( x))

Formal ergibt sich dieser Zusammenhang aus den Gesetzen der Aussagenlogik, wo beispielsweise die äquivalenzen P   ⇒ Q ≡ ¬P ∨  Q und ¬(P ∧ Q) ≡ ¬P ∨ ¬ Q gelten. Damit erhalten wir folgende Ableitung:

  1. Mensch(x) ⇒ ¬unfehlbar(x)
  2. ¬Mensch(x) ∨ ¬unfehlbar(x)
  3. ¬(Mensch(x) ∧ unfehlbar(x))

Die Ausdrücke (4.30.)(b) und (4.31.)(b) besagen das gleiche, sie sind äquivalent.

Nun kann man statt (4.29.) auch sagen

(4.32.)  (a) Es gibt keinen Menschen, der unfehlbar ist
(b) Es ist nicht der Fall, daß es ein x gibt, so daß gilt: x ist ein Mensch, und x ist unfehlbar
(c) ¬x (Mensch(x) ∧ unfehlbar( x))

Etwas anderes bedeutet

(4.33.) Nicht jeder Mensch ist glücklich

Dieser Satz kann folgendermaßen paraphrasiert werden:

(4.34.)  (a) Es ist nicht der Fall, daß alle Menschen glücklich sind
(b) ¬x (Mensch(x) ⇒ glücklich( x))

Die gleiche Bedeutung wie (4.34.) hat auch

(4.35.)  (a) Manche Menschen sind nicht glücklich
(b) Es gibt Menschen, die nicht glücklich sind
(c) x (Mensch(x) ∧ ¬glücklich( x))

Es besteht also ein enger Zusammenhang zwischen Allaussagen und Existenzaussagen, bei dem die Negation eine wichtige Rolle spielt. Man kann daher auch Regeln formulieren, nach denen Aussagen in andere Aussagen umgeformt werden können, ohne daß sich die Wahrheitsbedingungen ändern. So gelten z.B. allgemein folgende äquivalenzbeziehungen:

(4.36.)  (a) x P ≡ ¬x ¬P
 ("Für alle x gilt P" ist äquivalent mit "es gibt kein x für das P nicht gilt")
(b)x P ≡ ¬x ¬P
 ("Es gibt ein x für das P gilt" ist äquivalent mit "es ist nicht der Fall, daß für alle x P nicht gilt")

Diese äquivalenzen lassen sich formal auch noch folgendermaßen begründen: Wir haben gesehen, daß die Quantoren x und x sozusagen als "Summenzeichen" der Konjunktion bzw. der Disjunktion gelten können:

x p(x) ≡ p(a 1) ∧ p(a2) ∧  p(a3) ∧ … p( a n)

Nach dem Gesetz der Negation gilt dann auch:

¬¬(p(a1) ∧ p(a 2) ∧ p(a3) ∧ …) bzw.

¬[¬(p(a1) ∧ p( a2) ∧ p(a3) ∧ …)]

Aufgrund der Assoziativität der Konjunktion (P ∧ (Q ∧ R)) ≡ ( P ∧ Q) ∧ R ≡  P ∧ Q ∧ R können wir darauf schrittweise das Gesetz von de Morgan anwenden:

¬[¬p(a1) ∨ ¬(p( a2) ∧ p(a3) ∧ …)]

¬[¬p(a1) ∨ ¬p( a2) ∨ ¬(p(a3) ∧  p(a4) ∧ …)]

usw.

¬(¬p(a1) ∨ ¬p( a2) ∨ ¬(p(a3) ∨ ¬ p(a4) ∨ …)

¬x ¬p(x)

4.3. Relationen

Die bisher behandelten Aussagen bestehen entweder aus einer Individuenkonstante und einem Prädikat, sind also von der Form P(a), oder aus einer quantifizierten Verbindung von Aussageformen der Art P(x).

Die Aussage (4.37.) dagegen enthält zwei Individuenkonstanten: Peter und Fritz.

(4.37.) Peter ist größer als Fritz

Die Aussage (4.37.)hat die Form

(4.38.) x ist größer als y

wobei x und y Individuenvariablen sind. Den verbleibenden Teil ist größer als nennt man ebenfalls Prädikat. Ebenso ist der Ausdruck liegt zwischen ... und in (4.39.) ein Prädikat:

(4.39.)  (a) Bremen liegt zwischen Frankfurt und Hamburg
(b) x liegt zwischen y und z

Man kann also zwischen Aussagen mit einer Individuenkonstante und solche mit mehr als einer Individuenkonstante unterscheiden. Die entsprechenden Aussagenformen enthalten dann eine oder mehrere Leerstellen (Variablen). Man nennt die in diesen Aussagen bzw. Aussagenformen enthaltenen Prädikate daher jeweils einstellige, zweistellige, dreistellige etc. Prädikate.

Mehrstellige Prädikate stehen für Relationsbegriffe, d.h. für Begriffe, die irgendwelche Beziehungen zwischen Objekten repräsentieren. Man nennt mehrstellige Prädikate daher auch Relationen.

Auch Substantive können Relationen sein, z.B.:

(4.40.)  (a) Hans und Paul sind Brüder
(b) Hans ist Bruder von Paul

Aussagen mit Relationen (mehrstelligen Prädikaten) symbolisiert man ähnlich wie Aussagen mit einstelligen Prädikaten, indem man zuerst die Relation nennt und dahinter die Individuenkonstanten (bzw. Variablen) in Klammern setzt:

(4.41.)  (a) R(a, b)
(b) R(x, y)

Prädikate bezeichnen also

  • Allgemeinbegriffe (z.B. Pferd, Katze)
  • Eigenschaftsbegriffe (z.B. groß, rot)
  • Relationsbegriffe (z.B. größer als)

Wie muß nun eine Aussage (4.42.) analysiert werden?

(4.42.) Pferde sind größer als Kaninchen

Es wird ausgesagt, daß die Beziehung "x ist größer als y" zwischen jedem beliebigen Pferd einerseits und jedem beliebigen Kaninchen andererseits gilt. Anders ausgedrückt, jedes Element aus der Menge der Pferde ist größer als jedes Element aus der Menge der Kaninchen:

(4.43.)  (a) Für alle x und alle y gilt: wenn x ein Pferd ist und y eine Katze, dann ist x größer als y
(b) x y (Pferd(x) ∧ Katze( y) ⇒ größer als(x, y))

Man vergleiche auch

(4.44.)  (a) Manche Menschen gleichen sich
(b) Es gibt mindestens einen Menschen x und einen Menschen y, so daß gilt:
x gleicht y
(c) x y (M(x) ∧ M(y) ∧  G(x, y))

4.4. Die Syntax der Prädikatenlogik

Nach der vorangegangenen eher informellen Besprechung der sprachlichen Erweiterungen der Aussagenlogik in der Prädikatenlogik, können wir jetzt daran gehen, die Sprache der Prädikatenlogik durch genaue Syntaxregeln präzise zu definieren. Sie ist bestimmt durch eine Menge von Grundzeichen, einem Alphabet, und der Menge der (wohlgeformten) Formeln, die aus dem Alphabet konstruierbar sind.

Definition 4.2. Alphabet

Ein Alphabet besteht aus folgenden Symbolklassen:

Individuenvariable: x, y, z, x1…,y1…, z1…
Individuenkonstante: a, b, c, …, a1 …, b1…, c1…
Funktionen: f, g, h, f1 …, g1 …, h1 … mit verschiedener Stelligkeit >0.
Prädikaten: p, q, r, p1 …, q1 …, r1 … mit verschiedener Stelligkeit ³ 0.
Negation: ¬
Konjunktion und Disjunktion: ∧, ∨
Konditional und Bikonditional: ⇒, ⇔
Allquantor:
Existenzquantor:
Interpunktionszeichen: (, ), [, ], {,} und ",".

Zur Bezeichnung von Variablen, Konstanten, Funktionen und Prädikaten werden hier die üblichen Konventionen angenommen. Zur Beschreibung eines bestimmten Gegenstandsbereiches kann es sinnvoll sein, enger am Gegenstand orientierte Repräsentationsformen zu wählen.

Die Grundbausteine der Formeln werden Terme genannt.

Definition 4.3. Term

Ein Term wird induktiv wie folgt definiert:

  1. Jede Individuenvariable ist ein Term.
  2. Jede Individuenkonstante ist ein Term.
  3. Ist f eine n-stellige Funktion und sind t1, …, tn Terme, dann ist f(t1,…,tn) ein Term.
  4. Nur so gebildete Zeichenketten sind Terme.

Beispiele:

x, y (Variable)
a1, b2, cn (Konstante)
f(a), g(x, f(a,y), f(a, g(b, h(x,y)), f1(z)) (Funktionen)

Ist f(t1, …, tn) ein Funktionsterm, so heißen die Terme t1, …, tn die Argumente des Terms. Funktionen sind komplexe Repräsentationen von Individuen. Wofür eine Funktion steht, hängt von der Interpretation des Formalismus bezüglich eines bestimmten Gegenstands­bereiches ab.

Definition 4.4. Primformel

Ist p ein n-stelliges Prädikat und sind t1, …, tn Terme, dann ist p(t1, …, tn) eine Primformel.[4]

Beispiele:

p, q (0-stellige Prädikate)
p1(x), r(f(a)) (1-stellige Prädikate)
q2(f(a,b), g(x), s(x, f(y)) (2-stellige Prädikate)

Definition 4.5. Argument

Ist p(t1, …, tn) eine Primformel, so heißen die Terme t1, …, tn die Argumente der Primformel.

Prädikate unterscheiden sich von Funktionen dadurch, daß sie Wahrheitswerte repräsentieren.

Alle komplexen Formeln sind aus Primformeln zusammengesetzt:

Definition 4.6. Formel

Eine (wohlgeformte) Formel kann induktiv wie folgt definiert werden:[5]

  1. Primformeln sind Formeln.
  2. Ist F eine Formel so ist auch ¬F eine Formel.
  3. Sind F und G Formeln, so sind auch (F ∧ G), (F ∨ G), (F ⇒ G) und (F ⇔ G) Formeln. Für (F ⇒G) kann auch (G⇐ F) geschrieben werden.
  4. Ist F eine Formel und x eine Variable, dann sind (x F) und (x F) Formeln.

Beispiele

p, q  (0-stellige Primformeln)
p(x), q(y), r(a)  (1-stellige Primformeln)
(¬p(x))  
(p(a) ⇒ q(b)), (p(x) ⇔ q(x)), p(a) ∧ q(b)  
(x p(x)), (y (p(y) ∧ q( y))  

Die Bindungsbereiche der Quantoren ergeben sich aus der in der Definition aufgrund von (3.) verwendeten Klammerung.

Definition 4.7. Skopus 

Der Skopus (Bindungsbereich) von x (bzw. x) in x F (bzw. x F) ist F.

Definition 4.8. gebunden

Eine Variable kommt in einer Formel gebunden vor, wenn sie unmittelbar nach einem Quantor steht (z.B. x P oder x Q) oder wenn sie im Skopus eines Quantors mit der gleichen Variablen vorkommt (z.B. x p(x, y) bzw. y (p(y) ∧ q(y)).

Definition 4.9. frei

Eine Variable die nicht gebunden ist ist frei.

Beispiele

In der Formel x p(x, y) ∧ q(x) kommt x die ersten beiden Male gebunden vor, das dritte Mal frei, denn der Skopus von x ist p(x, y). In x (p(x, y) ∧ q(x)) kommt x nur gebunden vor, weil der Skopus von x jetzt p(x, y) ∧ q(x) ist.

Definition 4.10. Geschlossene Formel

Sind in einer Formel F alle Variablen durch Quantoren gebunden, gibt es also keine "freien" Variablen, dann wird F als geschlossene Formel bezeichnet.

Es gelten folgende Bindungsregeln

  • und binden stärker als ¬
  • ¬ bindet stärker als ∧
  • ∧ bindet stärker als ∨

Definition 4.11. Sprache erster Ordnung

Eine Sprache erster Ordnung bei einem gegebenen Alphabet besteht aus der Menge der Formeln, die aus den Symbolen des Alphabets nach den Regeln der Syntax gebildet werden können.

Beispiele:

(4.45.)  (a) (x (y (p(x,y) ⇒ q(x))))
(b) (¬(x (p(x,a) ∧ q( f(x)))))
(c) (x (p(x,g(x))  ( q(x) ∧ (¬r(x)))))
sind Formeln. Unter Berücksichtigung der Vorrangskala können diese wie folgt vereinfacht werden:
(4.46.)  (a) x y (p(x,y) ⇒ q( x))
(b) ¬x(p(x,a) ∧ q(f( x)))
(c) x(p(x,g(x))   q(x) ∧ ¬r(x))

4.5. Die Semantik der Junktoren und Quantoren

4.5.1. Junktoren

Die Junktoren (¬, ∧, ∨, ⇒, ⇔) haben in der Prädikatenlogik die gleiche Semantik wie in der Aussagenlogik.

4.5.2. Quantoren

x p(x) bedeutet "es gibt ein x das p(x) wahr macht", oder: p(a1) ∨ p(a2) ∨  p(a3) ∨…∨ p(a n)

x p(x) bedeutet "für alle x gilt, daß p(x) wahr ist", oder: p(a1) ∧ p(a2) ∧…∧  p(an).

x (p(x) ∧ ¬q( x) ⇒ r(x,g(x))) heißt also "für alle x gilt, wenn p(x) wahr ist und q(x) falsch, dann ist r(x, g(x)) wahr."

4.5.3. Äquivalenzen

FormelAbleitung
(1) x F ≡ ¬¬F x p(x)
p(a1) ∧ p(a2) ∧…∧  p(an)
¬(¬p(a1) ∨ ¬p( a2) ∨…∨ ¬p(a n))
¬¬p(x)
(2) x F ≡ ¬¬F x p(x)
p(a1) ∨ p(a2) ∨ … ∨  p(an)
¬(¬p(a1) ∧ ¬p( a2) ∧…∧ ¬p(a n))
¬x ¬p(x)
(3) x y F ≡ y x F
(4) x y F ≡ y x F
(5) x y F ⇒ y x F
(6) x (F ∧ G) ≡ x F ∧ x G
(7) x (F ∨ G) ≡ x F ∨ x G

4.6. Logisches Schließen im Rahmen der Prädikatenlogik

Eine wesentliche Aufgabe auch der Prädikatenlogik ist die Untersuchung der Gesetzmäßigkeiten des logischen Schließens, wobei sich durch all- bzw. existenzquantifizierte Aussagen besondere Probleme ergeben. Für nicht-quantifizierte Aussagen gelten die Schlußregeln der Aussagenlogik weiterhin.

Das Schließen mit allquantifizierten Aussagen soll an einem linguistischen Beispiel kurz erläutert werden. Im übrigen soll die Thematik, mit Ausnahme des Resolutionsprinzips im nächsten Abschnitt, nicht weiter vertieft werden.

Als Beispiel wählen wir eine kontexfreie Phrasenstruktur-Grammatik als Beschreibung der grammatischen Sätze eines Fragments der englischen Sprache. Die Sätze sind Ketten von englischen Wörtern, die bestimmte Bedingungen erfüllen, z.B. die, daß sie nach festen Regeln aus Teilketten aufgebaut sind.

(4.47.) Gegeben sei folgende Grammatik:

S  → NP ⁀ VP
NP → Det ⁀ N
NP → Name
VP → Vt ⁀ NP
VP → Vi
Det → the
N → boy
N → girl
N → ball
Name → John
Name → Mary
Vt → loves
Vt → kicked
Vi → jumped

Die Regel Satz→NP ⁀ VP ist etwa so zu interpretieren: Eine Wortkette z ist ein Satz gdw. sie sich so in zwei Teilketten x und y zerlegen läßt (d.h. z = x ⁀ y), daß x eine Nominalphrase (NP) und y eine Verbalphrase (VP) ist. Prädikatenlogisch ausgedrück heißt dies: 
x y (Satz(x ⁀ y) ⇐> NP(x) ∧ VP( y)).

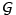
Wir können die Grammatik als ein Axiomensystem G auffassen, das aus einer Menge von Allaussagen und Einzelaussagen über Wortketten und Wörter besteht. Eine Wortkette ki ist dann ein grammatischer Satz, wenn die Aussage Satz(ki) aus dem Axiomensystem ableitbar ist, d.h. wenn gilt  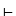 Satz( ki).

Die prädikatenlogische Interpretation dieser Grammatik sieht wie folgt aus:

(4.48.) R1: x y (NP(x) ∧ VP(y) ⇒  Satz(x ⁀ y))
R2: x y (Det(x) ∧ N(y) ⇒  NP(x ⁀ y))
R3: x (Name(x) ⇒ NP( x))
R4: x y (Vt(x) ∧ NP(y) ⇒  VP(x ⁀ y))
R5: x (Vi(x) ⇒ VP(x))
Lexikon:

Det(the)
N(boy)
N(girl)
N(ball)
Name(John)
Name(Mary)
Vt(loves)
Vt(kicked)
Vi(jumped)
Vi(laughed)

Es soll beispielsweise gezeigt werden, daß der Ausdruck the girl laughed ein grammatischer Satz ist. Dazu müssen wir mit den Regeln und dem Lexikon der Grammatik als Prämissen beweisen, daß die Ausage Satz(the ⁀ girl ⁀ laughed) aus der Grammatik G ableitbar ist, daß also gilt: G 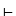 Satz( the ⁀ girl ⁀ laughed)

Beweis

(1) Det(the) Lexikon
(2)  N(girl) Lexikon
(3) Det(the) ∧ N(girl) (1),(2) Konjunktion
(4) Det(the) ∧ N(girl) ⇒  NP(the ⁀ girl) R2, Allbeseitigung
(5) NP(the ⁀ girl) (3),(4) Modus Ponens
(6) Vi(laughed) Lexikon
(7) Vi(laughed) ⇒ VP(laughed) R5, Allbeseitigung
(8) VP(laughed) (6),(7) Modus Ponens
(9) NP(the ⁀ girl) ∧ VP(laughed) (5),(8) Konjunktion
(10) NP(the ⁀ girl) ∧ VP(laughed) ⇒ Satz(the ⁀ girl ⁀ laughed) R1
(11) Satz(the ⁀ girl ⁀ laughed) (9),(10) Modus Ponens

4.7. Das Resolutionsprinzip in der Prädikatenlogik

Wir haben das Resolutionsprinzip bereits in der Aussagenlogik kennengelernt. Die Anwendung auf die Prädikatenlogik wird komplizierter durch die Existenz von quantifizierten Aussagen mit Individuenvariablen. Wir müssen für die Prädikatenlogik einige Begriffe neu definieren, den Algorithmus zur übersetzung von Formeln in die Klauselform erweitern, und die Bedingungen für die Anwendung des Resolutionsschemas präzisieren.

4.7.1. Klauselform

Die Begriffe Literal und Klausel müssen für die Prädikatenlogik neu definiert werden:

Definition 4.12. Literal

Ein Literal ist eine Primformel oder die Negation einer Primformel.

Beispiele für Literale sind p(x), q(f(a,b)),¬v(x,y).

Definition 4.13. Klausel

Eine Klausel ist eine Formel der Form x1…xs(L1 ∨…∨  Lm) wobei jedes Li ein Literal ist und x1,…, xs die einzigen Variablen sind, die in L1 ∨…∨ Lm vorkommen.

Beispiele: Die folgenden Formeln sind Klauseln

x y z (p(x,z) ∨ ¬ q(x,y) ∨¬r(y,z))

x y (¬p(x,y) ∨  r(f(x, y),a))

Für Klauseln gibt es eine besondere Schreibweise, die in der Logikprogrammierung verwendet wird. Man erhält sie, indem man zunächst die Literale nach positiven und negativen Literalen sortiert, z.B.

(4.49.) x1…xs(A1 ∨…∨  Ak ∨ ¬B1  ∨ …∨ ¬Bn)

Sei (4.49) eine Klausel mit den Primformeln A1,…, Ak, B1,…,Bn und x1,…,xs als den einzigen darin vorkommenden Variablen, so kann dafür

(4.50.) A1, …, Ak  B1, …, Bn

geschrieben werden.

Dies ergibt sich aus der äquivalenz von

(4.51.) x1…xs(A1 ∨…∨  Ak ∨¬B1 ∨…∨ ¬ Bn)

und

(4.52.) x1…xs(A1 ∨…∨  Ak  B1 ∧…∧  Bn)

und der Tatsache, daß alle vorkommenden Variablen allquantifiziert sind, so daß die Quantoren per Konvention weggelassen werden können.

Definition 4.14. Programmklausel

Eine Programmklausel ist eine Klausel der Form A  B1,…, Bn und enthält genau ein positives Literal (A). A ist der Kopf und B1,…,Bn der Rumpf der Programmklausel.

Definition 4.15. Einheitsklausel

Eine Einheitsklausel ist eine Klausel der Form A  d.h. eine Programmklausel mit leerem Rumpf.

Definition 4.16. Logikprogramm

Ein Logikprogramm ist eine endliche Menge von Programmklauseln.

Definition 4.17. Definition

In einem Logikprogramm ist die Menge aller Programmklauseln mit dem gleichen Prädikat p im Kopf die Definition von p.

Definition 4.18. Zielklausel

Eine Zielklausel ist eine Klausel der Form  B1,…, Bn d.h. eine Klausel ohne Kopf. Jedes Bi(i =1,…, n) ist ein Teilziel der Zielklausel.

Seien y1,…,yr die Variablen der Zielklausel ⇐ B1,…, Bn, dann ist dies eine Abkürzung für y1 … yr(¬B1 ∨…∨ ¬ Bn) oder, äquivalent dazu, ¬y1 … yr(B1 ∧…∧  Bn)

Definition 4.19. Leere Klausel 

Die leere Klausel , ist die Klausel ohne Kopf und Rumpf. Sie ist als Kontradiktion zu verstehen.

Definition 4.20. Horn Klausel 

Eine Horn Klausel ist eine Klausel, die entweder eine Programmklausel oder eine Zielklausel ist.

4.7.2. Umwandlung von Formeln in Klauselform

Bei der Umwandlung von Formeln in Klauselform gelten die gleichen Regeln wie für die Aussagenlogik, es kommen jedoch neue Regeln hinzu:

  1. Beseitigung des Bikonditionals (Bikond):   
    P ⇔ Q ≡ (P ⇒  Q) ∧ (Q ⇒ P)
  2. Beseitigung des Konditionals (Kond):       
    P ⇒ Q ≡ ¬P ∨  Q
  3. Skopus der Negation verringern (De Morgan):     
    ¬(P ∧ Q) ≡ ¬ P ∨ ¬Q     
    ¬(P ∨Q) ≡ ¬P ∧ ¬ Q      
    ¬x P(x) ≡ x ¬P(x)  
    ¬x P(x) ≡ x ¬P(x)
  4. Doppelte Negation beseitigen (Neg):        
    ¬¬P ≡ P
  5. Variablen umbenennen, so daß jeder Quantor eindeutig eine Variable bindet. Da Variablen nur Platzhalter sind, wird dadurch der Wahrheitswert der Formel nicht beeinflußt. Zum Beispiel, die Formel
    x P(x) ∨ x Q(x)       
    würde dadurch zu 
    x P(x) ∨ y Q(y)       
    umgewandelt werden. Dies dient der Vorbereitung für den nächsten Schritt
  6. Bringe die Formel in die Pränexe Normalform, indem alle Quantoren an den Anfang der Formel gestellt werden, ohne jedoch ihre relative Reihenfolge zu verändern. Dies ist möglich, weil es durch den vorherigen Schritt keine Namenskonflikte geben kann. Eine Pränexe Normalform besteht aus einem Präfix aus Quantoren gefolgt von einer quantorenfreien Matrix.
  7. Eliminiere die Existenzquantoren. Dies ist ein etwas schwierig nachzuvollziehender Schritt. Eine Formel wie z.B. x Bundeskanzler(x), die eine existenzquantifizierte Variable enthält, behauptet, daß es irgendein Indivduum gibt, das für x eingesetzt eine wahre Aussage ergibt. Wir wissen nicht, wer dieses Individuum ist, sondern nur, daß es existieren muß. Wir können diesem Individuum einen vorläufigen Namen geben — sagen wir s1 — und nehmen an, daß es für x eingesetzt die Existenzaussage wahr macht. Die Formel x Bundeskanzler(x) kann damit in Bundeskanzler(s1) transformiert werden. Man bezeichnet einen solchen "vorläufigen" Namen als Skolemkonstante. Die Beseitigung von Existenzquantoren durch Skolemkonstante bzw. Skolemfunktionen (s.u.) wird Skolemisierung genannt.
    Betrachten wir nun die Aussage "Jeder hat einen Vater": xy Vater(y,x). In diesem Falle steht der Existenzquantor im Skopus eines Allquantors. Es kann daher sein, daß der Wert von y, der das Prädikat erfüllen würde, in irgendeiner Weise vom Wert von x abhängig ist. In diesem Fall geht man davon aus, daß es eine Funktion gibt, die in Abhängigkeit von x den Wert von y bestimmt: y = s2(x). Man nennt eine solche Funktion eine Skolemfunktion.[6] Unsere Beispielformel kann damit in x Vater(s2( x),x) transformiert werden.
  8. Da jetzt alle noch verbleibenden Variablen allquantifiziert sind, kann das Präfix per Konvention weggelassen werden.
  9. Konvertiere die verbleibende Matrix in eine Konjunktion von Klauseln
    1. Konjunktion nach außen ziehen (Distributivgesetz der Disjunktion: Distrib):
      P ∨ (Q ∧ R) ≡ ( P ∨ Q) ∧ (P ∨  R)
    2. Gegebenenfalls Anwendung von Kommutativ- und Assoziativgesetzen (Komm, Assoz):
    3. Gegebenenfalls Vereinfachungen (Vereinf):
      1. P ∧ P ≡ P
      2. P ∨ P ≡ P
      3. P ⇒ P ≡  P
  10. Eine Konjunktion von Klauseln wird zu einer Klauselmenge zusammengefaßt. Falls mehrere Formeln zur Beschreibung des gleichen Sachverhalts dienen, werden sie nach der Konversion zu einer Klauselmenge zusammengefaßt.
  11. Gegebenenfalls Umbenennung der Variablen in der Klauselmenge nach dem vorigen Schritt, so daß keine zwei Klauseln die gleichen Variablen enthalten.

Beispiel:

 

Schritt Formel Kommentar
0 x y P(x,y)⇒¬y (Q(x,y) ⇒ R(x,y)) Ausgangsformel
1 x ¬y P(x,y)∨¬y (¬Q(x,y) ∨ R(x,y)) Konditional
2 x y ¬P(x,y)∨y (Q(x,y) ∧ ¬R(x,y)) Skopus der Negation
3 x y¬P(x,y)∨ z (Q(x,z) ∧ ¬R(x,z)) Variablen umbenennen
4 x ¬P(x,s1(x))∨ (Q(x,s2(x)) ∧ ¬R(x,s2(x))) Skolemisierung
5 ¬P(x,s1(x)) ∨ (Q(x, s2(x)) ∧¬R(x, s2(x))) Präfix weglassen
6

(¬P(x,s1(x)) ∨ Q(x, s2(x)) ∧ 

(¬P(x,s1(x)) ∨ ¬R(x, s2(x)))

Distribution
7

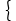¬P(x,s1(x)) ∨ Q(x, s2(x)),
¬P(x,s1(x)) ∨¬R(x, s2(x))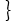

Klauselmenge
8

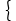¬P(x1,s1(x1)) ∨ Q(x1,s2(x1))

¬P(x2,s1(x2)) ∨ ¬R(x2, s2(x2))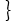

Variable umbenennen

Als weiterer Schritt wäre noch die Umformung zur Klauselnotation möglich gewesen, z.B. Q(x1,s2(x1)) ⇐  P(x1,s 1(x1)).

Die Umformung der Grammatik (4.48) in die Klauselform ist relativ einfach. Beispiel (R1):

(4.53.) x y (NP(x) ∧ VP(y) ⇒ Satz(x ⁀ y))         
x y (¬(NP(x) ∧ VP(y)) ∨ Satz(x ⁀ y)      
x y (¬NP(x) ∨ ¬VP(y) ∨ Satz(x ⁀ y)      
¬NP(x) ∨ ¬VP(y) ∨ Satz(x ⁀ y)
Satz(x ⁀ y) ⇐ NP(x), VP(y)

(4.54.) R1: ¬ NP(x1) ∨¬ VP(y1) ∨ Satz(x1 ⁀ y1)         
R2: ¬Det(x2) ∨ ¬N(y2) ∨ NP(x2 ⁀ y2)
R3: ¬Name(x3) ∨ NP(x3)       
R4: ¬Vt(x4) ∨¬ NP(y4) ∨ VP(x4 ⁀ y4)
R5: ¬Vi(x5) ∨ VP(x5)
Lexikon:
Det(the)
N(boy)
N(girl)
N(ball)
Name(John)
Name(Mary)
Vt(loves)
Vt(kicked)
Vi(jumped)
Vi(laughed)

In Klauselnotation

(4.55.) R1: Satz(x1 ⁀ y1) NP(x1), VP(y1)     
R2: NP(x2 ⁀ y2) Det(x2), N(y2)         
R3: NP(x2)⇐ Name(x3)         
R4: VP(x4 ⁀ y4) Vt(x4), NP(y4)         
R5: VP(x5) Vi(x5)    
Lexikon:
       Det(the)
       N(boy)
       N(girl)
       N(ball)
       Name(John)
       Name(Mary)
       Vt(loves)
       Vt(kicked)
       Vi(jumped)
       Vi(laughed)

4.7.3. Substitution und Unifikation

Für die Anwendung des Resolutionsschemas auf zwei Klauseln ist Voraussetzung, daß ein Literal in einer Klausel positiv, in der anderen negativ vorkommt. In Rahmen der Prädikatenlogik entsteht ein Problem dadurch, daß Formeln erst durch die Substitution von Variablen verlgeichbar werden. Nehmen wir beispielsweise das folgende Paar

(4.56.) ¬ Vi(x5) ∨ VP(x5)
Vi(laughed)

Das Resolutionsschema kann hier erst angewandt werden, wenn man die Variable x5 durch laughed substituiert.

(4.57.) ¬Vi(laughed) ∨ VP(laughed)
Vi(laughed)
VP(laughed) Resolvente

Das Verfahren, durch das festgestellt wird, ob zwei Ausdrücke durch geeignete Substitutionen für ihre Variablen gleich gemacht werden können, nennt man Unifikation. Die Möglichkeit der Unifikation ist eine Grundvoraussetzung für die Anwendung des Resolutionsprinzips in der Prädikatenlogik.

Definition 4.21. Substitution

Eine Substitution θ ist eine endliche Menge der Form {v1/t1, …, v n/tn}, wobei jedes vi eine Variable und jedes ti ein von vi verschiedener Term ist und die Variablen v1, …,vn verschieden sind. Man sagt die vi werden durch die ti substituiert bzw. an sie gebunden. Jedes Element vi/ti ist eine Bindung für vi.

Definition 4.22. Ausdruck

Ein Ausdruck ist entweder ein Term oder eine Formel. Ein einfacher Ausdruck ist entweder ein Term oder eine Primformel.

Definition 4.23. Substitutionsinstanz

Sei φ ein Ausdruck und θ={v1/t1, …,  vn/tn} eine Substitution. Die Anwendung von θ auf φ, geschrieben φθ, ist der Ausdruck, der entsteht, wenn in φ die vi gleichzeitig durch die ti ersetzt werden (Substitutionsinstanz). Man sagt auch, die Variablen vi in φ werden zu den Werten ti instantiiert.

Beispiel: θ = {x5/laughed}, φ = ¬Vi(x5) ∨  VP(x5),     und jq = ¬Vi(laughed) ∨ VP( laughed)

Definition 4.24. Komposition

Seien θ = {u1/s1,…, um/sm} und σ = {v1/t 1, …, vn/tn} Substitutionen. Die Komposition (Hintereinanderausführung) σ von θ und σ ist die Substitution, die man aus der Menge

{u1/s1σ,…,u m/smσ, v1/t1,…,vn/ tn}

erhält, indem man alle Bindungen ui/siσ entfernt, für die ui = siσ und alle Bindungen vj/tj, für die vj Î {u1, …,  um}

Beispiel:

Sei θ = {x/f(y), y/z} und σ={x/a, y/b, z/y}; x/f(y) entspricht u1/s1, y/z entspricht u2/s2.

Dann erhält man σ aus {x/f(y)σ, z/yσ} È σ wie folgt:

            {x/f(y){x/a, y/b, z/y},   y/z{x/a, y/b, z/y},       x/a, y/b, z/y}

                       

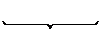
                        x/f(b)                           y/y

Die unterstrichenen Terme fallen weg, also gilt: σ = {x/f(b), z/y}

Definition 4.25. leere Substitution 

Die leere Substitution ist durch die leere Menge {  } gegeben und wird mit ε bezeichnet. Ist φ ein Ausdruck, so gilt φε=φ.

Definition 4.26. Varianten

Seien φ und ψ Ausdrücke. φ und ψ sind Varianten, wenn es zwei Substitution θ und σ gibt derart, daß φ=ψθ und ψ=js. Man sagt φ sei eine Variante von ψ und umgekehrt.

Beispiel: p(f(x,y), g(z),a) ist eine Variante von p(f(y,x), g(u),a). Dabei ist θ={y/x, x/y, u/z} und σ={x/y, y/x, z/u}.

Varianten lassen sich durch Umbenennung der Variablen in einander überführen.

Von besonderem Interesse sind Substitutionen, die eine Menge von Ausdrücken gleich machen (unifizieren).

Definition 4.27. unifizierbar

Eine Menge von Ausdrücken {φ1,…,φn} heißt unifizierbar, wenn es eine Substitution θ gibt, welche alle Ausdrücke gleich macht, d.h. φ1θ=…=φn θ.

Beispiel: die Substitution {x/A, y/B, z/C} unifiziert die Ausdrücke P(A,y,z) und P(x,B,z) mit dem Ergebnis P(A,B,C)

P(A,y,z){x/A, y/B, z/C}=P(A,B,C)=P(x,B,z){x/A,y/B, z/C}

Definition 4.28. Unifikator

Eine Substitution θ heißt Unifikator für eine Menge von Ausdrücken {φ1,…,φn} falls diese dadurch unifiziert werden, d.h. wenn gilt {φ1,…,φn}θ={ ψ} wobei ψ = φ1θ = … =  φnθ.

Obwohl die Substitution {x/A, y/B, z/C} die beiden Ausdrücke P(A,y,z) und P(x,B,z) unifiziert, ist sie nicht der einzige Unifikator. Da die Variable z in beiden Ausdrücken an der gleichen Argumentstelle vorkommt, muß sie nicht substituiert werden, um die Gleichheit zu erreichen. Mit der Substitution {x/A, y/B} wären die Ausdrücke ebenfalls unifizierbar gewesen.

P(A,y,z){x/A, y/B}=P(A,B,z)=P(x,B,z){x/A,y/B}

Der Unifikator {x/A, y/B} ist allgemeiner als der Unifikator {x/A, y/B, z/C}. Intuitiv ist ein Unifikator umso allgemeiner, je weniger Variable bei der Unifikation substituiert werden. Die Substitution {z/F(w)} ist allgemeiner als {z/F(C)}. Eine Substitution θ ist allgemeiner als eine Substitution σ gdw. es eine andere Substitution d gibt derart, daß θd=σ. Im Beispiel: {z/F(w)}{w/C}={z/F(C)}.

Definition 4.29. allgemeinster Unifikator 

Sei S eine endliche Menge von einfachen Ausdrücken. Ein Unifikator θ für S heißt allgemeinster Unifikator für S (engl. most general unifier (mgu)), wenn es für jeden weiteren Unifikator σ von S eine Substitution g gibt derart, daß σ=θg.

Beispiel: Die Ausdrucksmenge {p(f(x),z), p(y,a)} ist unifizierbar beispielsweise durch den Unifikator σ={y/f(a),x/a,z/a}. p(f(x),z)σ=p(f( a),a)=p( y,a)σ. Ein allgemeinster Unifikator ist θ={y/f(x),z/a}. Es gilt σ=θ{x/a}.

Unifikationsalgorithmus

Eingabe: zwei einfache Ausdrücke φ und ψ

Ausgabe: der allgemeinste Unifikator von φ und ψ

Sind φ und ψ gleiche Konstanten oder gleiche Variable, so sind sie mit der leeren Substitution {  } unifizierbar. Sind sie verschiedene Konstante schlägt die Unifikation fehl.

Ist φ eine Variable, die nicht in ψ vorkommt, so sind φ und ψ mit der Substitution {φ/ψ} unifizierbar. Kommt φ in ψ vor, so schlägt die Unifikation fehl.

Sind φ und ψ Funktionen mit gleichem Funktor und gleicher Stelligkeit (Argumentzahl) (f(s1,…, sn) bzw. f(t1,…,tn)) so sind sie unifizierbar, wenn jedes Argumentpaar ti, si, i=1 … n unifizierbar ist. Andernfalls schlägt die Unifikation fehl.

Definition 4.30. Unterschiedsmenge

Sei A eine endliche Menge von einfachen Ausdrücken. Die Unterschiedsmenge (engl. disagreement set) von A ist wie folgt definiert. Ermittle die am weitesten links stehende Symbolposition an der nicht alle Ausdrücke in A das gleiche Symbol haben und extrahiere aus jedem Ausdruck in A den Teilausdruck, der an dieser Symbolposition beginnt. Die Menge all dieser Teilausdrücke ist die Unterschiedsmenge.

Beispiel: Sie A={p(f(x), h(y), a), p(f(x), z, a), p(f(x), h(y), b)}. Dann ist die Unterschiedsmenge {h(y), z}.

Ein Unifikationsalgorithmus kann auf dieser Grundlage präziser und einfacher wie folgt angegeben werden (A sei eine endliche Menge von einfachen Ausdrücken):

Unifikationsalgorithmus

  1. Setze k=0 und θ0=ε
  2. Wenn Aθk (d.h. die Anwendung von θk auf A) eine Einermenge ist (nur aus einem Element besteht), dann halt; θk ist der allgemeinste Unifikator von A. Andernfalls ermittle die Unterschiedsmenge Dk von Aθk.
  3. Gibt es ein v und ein t in Dk, so daß v eine Varialbe ist, die in t nicht vorkommt, dann setze θk+1 = θk{v/t}, erhöhe k um 1 und gehe zu 2. Andernfalls halt; A ist nicht unifizierbar.
  4. Beispiel: Sei A={p(a , x, h(g(z))), p(z, h(y), h(y))}
    1. θ0=ε
    2. D0={a,z}, θ1={z/a}, und Aθ1={p(a, x, h(g(a))), p(a, h(y), h(y))}.
    3. D1={x, h(y)}, θ2={z/a, x/h(y)} und Aθ2={p(a,h(y), h(g(a))), p(a,h(y), h(y))}.
    4. D2={g(a), y}, θ3={z/a, x/h(g(a)), y/g(a)} und Aθ3={p(a,h(g( a)),h(g(a)))}.
      Also ist A unifizierbar und θ3 ist ein allgemeinster Unifikator.

4.8. Anwendungsbeispiel

Zur besseren Vergleichbarkeit soll das gleiche Beispiel wie in Abschnitt 3. verwendet werden: the girl laughed. Es soll also nach dem Resolutionsverfahren bewiesen werden, daß die Aussage Satz(the ⁀ girl ⁀ laughed) wahr ist. Wir legen dafür die gleiche Grammatik zugrunde, allerdings in Klauselnotation. Der Bequemlichkeit halber soll sie hier noch einmal wiederholt werden:

(4.58) PS-Grammatik in Klauselnotation
R1: Satz(x1 ⁀ y 1)NP(x1), VP(y1)
R2: NP(x2 ⁀ y 2)Det(x2), N(y2)
R3: NP(x3)Name(x3)
R4: VP(x4 ⁀ y 4)Vt(x4), NP(y4)
R5: VP(x5)Vi(x5)
Lexikon:
Det(the)
N(boy)
N(girl)
N(ball)
Name(John)
Name(Mary)
Vt(loves)
Vt(kicked)
Vi(jumped) Vi(laughed)

Damit die Resolution durchgeführt werden kann, ist erforderlich, daß in zwei verschiedenen Klauseln ein Literal einmal positiv und einmal negativ vorkommt. Hier zeigt sich der syntaktische Vorteil von Programmklauseln, insofern nur der Kopf ein positives Literal sein kann, während der Rumpf nur aus negativen Literalen besteht. Zur Beseitigung eines Literals aus dem Rumpf einer Klausel müssen wir versuchen, dieses mit dem Kopf einer Programm­klausel zu unifizieren.

Die Prämissen sind die Programmklauseln (einschließlich Einheitsklauseln) der Grammatik. Gemäß dem Verfahren des indirekten Beweises nehmen wir zunächst die Negation der zu beweisende Aussage zu den Prämissen hinzu.

(4.59.) ¬Satz(the ⁀ girl ⁀ laughed)

Es handelt sich um ein negatives Literal, so daß wir die Klauselnotation

(4.60.) Satz(the ⁀ girl ⁀ laughed),

d.h. eine Zielklausel, erhalten. Im folgenden Beweis steht Z für Zielklausel, P für Programmklausel, U für Unifikator und R für Resolvente. Die Resolvente ist jeweils die Zielklausel für den nächsten Schritt:

 

Z:   Satz(the ⁀ girl ⁀ laughed)
P: Satz(x1 ⁀ y1) NP(x 1), VP(y1)
U: {x1/the ⁀ girl, y1/laughed}  
R:   NP(the ⁀ girl), VP(laughed)
Z = R:    
P: NP(x4 ⁀ y4) Det(x 4), N(y4)
U: {x4/the, y4/girl} Det(the) , N(girl), VP(laughed)
R:    
Z = R:    
P:  Det(the)
U: ε N(girl) , VP(laughed)
R:    
Z = R: N(girl)
P:    
U:  ε  
R:   VP(laughed)
Z = R:    
P: VP(x5) Vi(x 5)
U: {x5/laughed}  
R:   Vi(laughed)
Z = R:    
P:  Vi(laughed)
U:  ε  
R:   

 

Im folgenden Beispiel geht es um die zunächst merkwürdig erscheinende Frage, ob es überhaupt Ketten gibt, die nach der Grammatik zugelassen sind. Wir gehen aus von der Behauptung x Satz( x). Die Negation dieser Behauptung, ¬ x Satz( x), wird als zusätzliche Prämisse übernommen. Sie muß zunächst unter Verwendung der äquivalenz ¬ x P(x) ≡ x ¬P(x) in Klauselform übersetzt werden. Das Ergebnis, x  ¬Satz(x), hat die Klauselform  Satz(x). Der Beweis sieht dann wie folgt aus:

Z:   Satz(x)
P: Satz(x1 ⁀ y1)  NP(x 1), VP(y1)
U: {x/x1 ⁀ y1}  
R:   NP(x 1), VP(y1)
Z = R:    
P: NP(x3) Name(x3)
U: {x1/x3}  
R:    Name(x 3), VP(y1)
Z = R:     
P:  Name(Mary) 
U:  {x3/Mary}  
R:   VP(y 1)
Z = R:    
P:  VP(x5) Vi(x 5)
U:  {y1/x5}  
R:   Vi(x 5)
Z = R:    
P: Vi(jumped)
U: {x5/jumped}  
R:  

 

Von Interesse ist hier primär nicht die Tatsache, daß die Behauptung x Satz( x) beweisbar ist, sondern daß auch eine Instanz für x geliefert wird, die man erhält, wenn man die Komposition der Unifikatoren bildet:

(4.61.) Komposition der Unifikatoren

{x/x1 ⁀ y 1}{x1/x3 }{x3/Mary}{y1/x 5}{x5/jumped}

{x/x3 ⁀ y 1}{x3/Mary}{y1 /x 5}{x5/jumped}

{x/Mary ⁀ y 1}{y1/x5}{x 5 /jumped}

{x/Mary ⁀ x5 }, x5/jumped}

{x/Mary ⁀ jumped}

Mit anderen Worten, im Zuge des Beweises werden durch Unifikation Variablen gebunden und damit Sätze generiert. Jeder alternative Beweisweg generiert einen anderen Satz.

4.9. Definite Clause Grammar (DCG)

4.9.1. Verkettung

Wir waren bisher davon ausgegangen, daß in einer Regel wie

(4.62.) Satz(x ⁀ y) NP(x), VP(y)

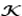
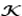
eine Verkettungsoperation definiert ist, die Paare von Ketten auf Ketten abbildet ( 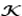, wenn 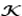die Menge aller möglichen Ketten ist) und ein funktionales Argument wie x ⁀ y entsprechend ausgewertet wird. Dies ist jedoch insbesondere in Prolog nicht gegeben.[7]

Es gibt aber eine Möglichkeit, die Verkettung ausschließlich über die Unifikation von Termen zu beschreiben. Dazu benötigen wir zunächst eine präzise Definition des Begriffs Kette:

Definition 4.31. Kette 

Eine Kette kann induktiv wie folgt definiert werden

1. Der Term nil ist eine Kette, die leere Kette.

2. Ist R eine Kette und K ein Term, dann ist K.R eine Kette. K ist der Kopf und R der Rumpf der Kette.

Ein Ausdruck wie the girl laughed wird damit als the.girl.laughed.nil notiert.

Die Behandlung der Verkettung (bzw. umgekehrt der Zerlegung von Ketten in Teilketten) beruht auf folgender überlegung: Ein Kette k0 enthält am Anfang einen Satz mit einem Rest k (d.h. Satz(k0–k)), wenn es eine Anfangskette k0–k1 gibt, für die gilt NP(k0–k1) und die Restkette k1 eine Kette k1–k mit VP(k1–k) enthält. Die gesamte Kette k0 ist ein Satz, wenn die Restkette k leer ist. Die leere Kette soll mit der Konstante nil bezeichnet werden.

 

k0

k0–k

k

k0–k1

k1

 

k1–k

k

k0
the.girl.laughed.nil

k0–k
the.girl.laughed

k
nil

k0–k1
the.girl

k1
laughed.nil

 

k1–k
laughed

k
nil

Der entscheidende Punkt ist dabei, daß im Falle eines terminalen Symbols t gilt: k0=t.k. Die Zerlegung einer Kette in Teilketten wird damit zurückgeführt auf die Zerlegung der Kette in das erste terminale Element und die Restkette. Die Differenzketten[8] wie k0–k werden im folgenden durch zwei Argumente dargestellt, so daß die erste Syntaxregel wie folgt formuliert werden kann:

(4.63.) Satz(k0,k)NP(k0,k1) , VP(k1,k)

Lexikonregeln hätten die Form LK(k0,k), wobei jedoch gilt k0=Wort.k, z.B.:

(4.64.) Det(the.k,k)

Unsere PS-Grammatik erhält damit die folgende Form, wobei die Variablen für die spätere Anwendung bereits durch Indizes umbenannt worden sind:

(4.65.) PS-Grammatik in Klauselnotation mit Differenzketten
R1: Satz(x1, z1)NP(x1,y1) , VP(y1,z1)
R2: NP(x2, z2)Det(x2,y2) , N(y2,z2)
R3: NP(x3,z3)Name(x3,z3)
R4: VP(x4, z4)Vt(x4,y4) , NP(y4,z4)
R5: VP(x5,z5)Vi(x5,z5)
Lexikon:
       Det(the.z6,z6)
       N(boy.z7,z7)
       N(girl.z8,z8)
       N(ball.z9,z9)
       Name(John.z10,z10)
       Name(Mary.z11,z11)
       Vt(loves.z12,z12)
       Vt(kicked.z13,z13)
       Vi(jumped.z14,z14)
       Vi(laughed.z15,z15)

Die der Behauptung "John kicked the ball ist ein Satz" entsprechende Zielklausel hat jetzt die Form

(4.66.) Satz(John.kicked.the.ball.nil,nil)

Der Beweis erhält nunmehr die in (4.67.) gezeigte Form.

(4.67.)

Z:   Satz(John.kicked.the.ball.nil,nil) 
P:   Satz(x1,z1) NP(x1,y1) , VP(y1,z1)
U:  {x1/John.kicked.the.ball.nil,z1 /nil}  
R:   NP(John.kicked.the.ball.nil,y 1),VP(y1,nil)
Z = R:    
P:  NP(x3, z3) Name(x3,z3)
U: {x3/John.kicked.the.ball.nil, z3/y1}  
R:   Name(John.kicked.the.ball.nil,y1) , VP(y1,nil)
Z = R:    
P: Name(John.z10,z10)  
U: {z10/kicked.the.ball.nil, y1/kicked.the.ball.nil}  
R:   VP(kicked.the.ball.nil,nil)
Z = R:    
P:  VP(x4, z4) Vt(x4,y4) ,NP(y4,z4)
U:  {x4/kicked.the.ball.nil, z4/nil}  
R:   Vt(kicked.the.ball.nil,y4) , NP(y4,nil)
Z = R:    
P:  Vt(kicked.z13,z13)
U:  {z13/the.ball.nil, y4/the.ball.nil}  
R:   NP(the.ball.nil,nil)
Z = R:    
P: NP(x2,z2)  Det(x2,y2) ,N(y2,z2)
U:  {x2/the.ball.nil, z2/nil}  
R:    Det(the.ball.nil, y2), N(y2, nil)
Z = R:    
P:  Det(the.z6,z6) 
U:  {z6/ball.nil,y2/ball.nil}  
R:    N(ball.nil,nil)
Z = R:    
P:  N(ball.z9,z9) 
U:  {z9/nil}  
R:    

 

> 4.9.2. Der DCG-Formalismus

Nachdem nun der Beweismechanismus der hier diskutierten Form der Logikgrammatik (hoffentlich) deutlich geworden ist, können wir dazu übergehen, diesen Mechanismus vor dem Grammatiker zu “verstecken”.

Wir haben gesehen, daß eine PS-Regel wie Satz → NP VP in der Klauselnotation der Logikgrammatik als Satz(k0,k)NP(k 0,k1) , VP(k1,k) wiedergegeben wird. Lexikonregeln, die nichtterminale lexikalische Kategorien zu terminalen Symbolen expandieren, werden zu Einheitsklauseln, d.h. eine Regel wie Vt → kicked wird zu Vt(kicked.k,k). Es ist nunmehr möglich, übersetzungsregeln zu formulieren, die PS-Regeln in Regeln der Logikgrammatik überführen: Ein Ausdruck wie  
A → B C wird übersetzt in A(k0,k)B(k0 ,k1) , C(k1,k)

Allgemein soll gelten:

  1. Seien A, B1,…,Bn nichtterminale Symbole und ki Variable über Wortketten, so gilt
    A → B1 … Bn wird übersetzt in
    A(k0,kn) B1(k0 ,k1),…, Bi(ki–1,ki) ,…, Bn(kn–1,kn),
    wobei für kn einfach k geschrieben werden kann.
  2. Sind A und Bi nichterminale Symbole und ist a ein Terminalsymbol so gilt:
    A → a wird übersetzt in A(a.k,k);
    … Bi a … wird übersetzt in …, Bi(ki–1,a.ki) , …

Unter Berücksichtigung dieser übersetzungsregeln kann eine DCG im wesentlichen in der bekannten Form der PSG formuliert werden.[9]

Nun ist mehrfach gezeigt worden, daß kontextfreie Phrasenstrukturgrammatiken in dieser einfachen Form nicht deskriptiv adäquat sind. Der DCG-Formalismus enthält daher auch zwei wesentliche Erweiterungen, die seine Expressivität und Mächtigkeit erheblich vergrößern:

  1. Nichtterminale Symbole sind nicht atomar, sondern können durch eine beliebige Zahl von Argumenten aus Termen beliebiger Komplexität erweitert werden, die der Unifikation unterliegen, z.B.
    Satz → NP(num,pers),VP(num,pers).
  2. Es können beliebige Bedingungen (constraints) in Form von zusätzlichen Literalen (bzw. Klauseln) hinzugefügt werden. Diese bleiben bei der übersetzung erhalten, und werden durch geschweifte Klammern gekennzeichnet, z.B.
    Satz → NP(typ1),VP(typ2) ,{ subtyp(typ1,typ2)}

Wir benötigen entsprechend zusätzliche übersetzungsregeln:

  1. A(xι,…,xν) → … wird übersetzt in A(x ι ,…,xν,k0,k)…
    Bi(xι,…,x ν) wird übersetzt in Bi(x ι,…,xν,k i–1, ki)
  2. {B1,…, Bn} wird übersetzt in B1, …, Bn

Zusätzliche Argumente können beispielsweise dazu verwendet werden, Abhängigkeiten der verschiedensten Art zu formulieren. Eine Regel wie

(4.68.) Satz → NP(num,pers), VP(num,pers)
(in der übersetzung: Satz(k0,k) NP(num,pers,k0,k1) ,VP(num,pers, k1,k))

drückt z.B. den Sachverhalt aus, daß Subjekt und Prädikat hinsichtlich der grammatischen Kategorien Numerus und Person übereinstimmen müssen.

Da die Argumente beliebig komplexe Terme sein können, ist es möglich, gleichzeitig mit der Konstruktion eines Beweises Strukturbeschreibungen durch Unifikation aufzubauen. Unsere Beispielgrammatik erhält dadurch folgende Form:

(4.69.) DC-Grammatik mit zusätzlichem Argument zur Strukturbeschreibung

R1: Satz(S(np0,vp))→ NP(np0), VP(vp)
R2: NP(NP(d,n))→ Det(d), N(n)
R3: NP(NP(name))→ Name(name)
R4: VP(VP(vt,np1)→ Vt(vt), NP(np1)
R5: VP(VP(vi))→ Vi(vi)
Lexikon:
            Det(Definite)→ the
            N(N(boy))→ boy
            N(N(girl))→ girl
            N(N(ball))→ ball
            Name(N(John))→ John
            Name(N(Mary))→ Mary
            Vt(Vt(love))→ loves
            Vt(Vt(kick))→ kicked
            Vi(Vi(jump))→ jumped
            Vi(Vi(laugh))→ laughed

Nach unseren übersetzungsregeln erhalten wir daraus das folgende Logikprogramm:

(4.70.) DCG in Klauselnotation mit zusätzlichem Argument zur Strukturbeschreibung

            R1: Satz(S(np1,vp),x1 , z1) NP(np1,x 1,y1), VP(vp,y1,z1)
R2: NP(NP(d,n),x2, z2)Det(d,x2,y2) , N(n,y2,z2)
R3: NP(NP(name),x3,z3)Name(name,x3,z 3)
R4: VP(VP(vt,np2),x4, z4)Vt(vt,x4,y4) , NP(np2,y4,z4)
R5: VP(VP(vi),x5,z5)Vi(vi,x5,z5)
Lexikon:
       Det(Det(Definite),the.z6,z 6)
       N(N(boy),boy.z7,z7)
       N(N(girl),girl.z8,z8)
       N(N(ball),ball.z9,z9)
       Name(N(John),John.z10,z 10)
       Name(N(Mary),Mary.z11,z 11)
       Vt(Vt(love),loves.z12,z 12)
       Vt(Vt(kick),kicked.z13,z 13)
       Vi(Vi(jump),jumped.z14,z 14)
       Vi(Vi(laugh),laughed.z15,z 15)

Die folgende Seite zeigt die Ableitung des Satzes John kicked the ball mit gleichzeitiger Konstruktion einer Strukturbeschreibung. Die mit S: bezeichnete Zeile zeigt nach jedem Resolutionsschritt die Strukturbeschreibung nach Anwendung des Unifikators auf den vorherigen Output. Zu beweisen ist die Aussage: sb Satz( sb, John.kicked.the.ball.nil,nil), d.h. die Zielklausel        
⇐Satz(sb,John.kicked.the.ball.nil,nil).

Z:      Satz(sb,John.kicked.the.ball.nil,nil)
P:    Satz(S(np1,vp),x 1 ,z1) NP(np1,x1 ,y1),VP(vp,y1,z 1)
U: {sb/S(np1,vp),x1 /John.kicked.the.ball.nil,z 1/nil}  
S:   S(np1,vp)  
R:    NP(np1,John.kicked.the.ball.nil,y 1),VP(vp,y1,nil)
Z = R:    
P:  NP(NP(name),x3,z 3) Name(name,x3,z 3)
U: {np1/NP(name),x3 /John.kicked.the.ball.nil,z 3/y1}  
S:  S(NP(name),vp)  
R:    Name(name, John.kicked.the.ball.nil,y1),VP(vp,y 1,nil)
Z = R:    
P:  Name(N(John),John.z10,z 10)
U: {name/N(John),z10/kicked.the.ball.nil,y 1/kicked.the.ball.nil}.  
S:  S(NP(N(John)), vp)  
R:      VP(vp,kicked.the.ball,nil)
Z = R:    
P:  VP(VP(vt,np2),x4 ,z 4) Vt(vt,x4 ,y4),NP(np2,y 4 ,z4)
U:  {vp/VP(vt,np2), x4/kicked.the.ball.nil,z4/nil}  
S:   S(NP(N(John)),VP(vt,np 2))  
R:      Vt(vt,kicked.the.ball.nil,y 4),NP(np2,y4 ,nil)
Z = R:    
P:  Vt(Vt(kick),kicked.z13,z 13)
U: {vt/Vt(kick),z13/the.ball.nil,y 4/the.ball.nil}  
S:  S(NP(N(John)),VP(Vt( kick) ,np2))  
R:    NP(np2,the.ball.nil,nil)
Z = R:    
P:  NP(NP(d,n),x2,z 2)  Det(d,x2,y2) ,N(n,y2,z2)
U:  {np2/NP(d,n),x2 /the.ball.nil,z 2/nil}  
S:  S(NP(John),VP(Vt(kick) ,NP( d,n)))  
R:    Det(d,the.ball.nil,y2) ,N(n,y2,nil)
Z = R:    
P:  Det(Det(Definite),the.z6 ,z 6)
U:  {d/Det(Definite),z6/ball,nil,y 2/ball.nil}  
S: S(NP(John),VP(Vt(kick) ,NP( Det(Definite),n)))  
R:    N(n,ball.nil,nil)
Z = R:    
P:  N(N(ball),ball.z9,z 9)
U: {n/N(ball),z9/nil^  
S:  S(NP(John),VP(Vt(kick) ,NP( Det(Definite),N(ball))))  
R:   

Durch Regeln wie

(4.71.)

S → NP(typ0),VP(typ1),{ Subtyp(typ0,typ1}

VP(typ1) → Vt(typ1,typ2),NP( typ 3),{Subtyp(typ3,typ2)}
Vt(Person,Universal) → admired

N(Person) → John
N(Idea) → sincerity

werden Kontextabhängigkeiten zwischen dem Verb und seinen Aktanten ausgedrückt, die z.B. John admired sincerity zulassen, *Sincerity admired John aber ausschließen. Das Prädikat Subtyp kann dabei z.B. auf eine Typhierarchie Bezug nehmen.

In ähnlicher Weise ließe sich eine Semantik im Stile von Montague in die DCG integrieren.

Literatur

Abramson, Harvey & Dahl, Vernonica

1989       Logic Grammars. Springer-Verlag: New York etc.

Bates. M.

1978       The Theory and Practice of Augmented Transition Network Grammars. In: Bolc (1978), 191–259.

Bolc, Leonard (ed.)

1978       Natural Language Communication with Computers. Springer Verlag: Berlin.

Colmerauer, Alain

1978       Metamorphosis Grammars. In Bolc(1978), 1933–89.

Grosz, Barbara J., Karen Sparck Jones, & Bonnie Lynn Webber, eds.

1986       Readings in Natural Language Processing. Morgan Kaufmann: Los Altos, California.

Lloyd, J.W.

1984       Foundations of Logic Programming. Springer-Verlag: Berlin etc.

Pereira, Fernando C.N. & Stuart M. Shieber

1987       Prolog and Natural-Language Analysis. Center for the Study of Language and Information: Stanford.

Pereira, Fernando C. N. & David H. D. Warren

1980       Definite clause grammars for language analysis — a survey of the formalism and a comparison with augmented transition networks. In: Artificial Intelligence 13:231–278. (Reprint in Grosz et. al. 1986).

Robinson, J.A.

1965       A machine-oriented logic based on the resolution principle. In: Journal of the ACM 12:23–44.

Woods, W. A.

1970       Transition Network Grammars for Natural Language Analysis. In: Communications of the ACM 3: 591–606. (Reprint in Grosz et al. 1986: 71–87.)

 

[1] Man kann die Aussagenlogik auch als einen Grenzfall der Prädikatenlogik betrachten.

[2]  Es gibt andere Konventionen zur Wiedergabe von "für alle x gilt P", z.B. (x) P und ∀x P.

[3]  Eine alternative Konvention für den Existenzquantor ist ∃x p( x).

[4]  Primformeln werden auch atomare Formeln oder Atome genannt.

[5]  änderungen im Vergleich zur Aussagenlogik sind eingerahmt.

[6]  Benannt nach einem norwegischen Mathematiker namens Skolem. Skolemkonstante sind Skolemfunktionen mit Null Argumenten.

[7]  In Prolog sind Funktionen im prädikatenlogischen Sinne bloße syntaktische Strukturen, die nicht ausgewertet werden.

[8]  In Prolog werden Ketten als Listen dargestellt. Man spricht dort entsprechend von Differenzlisten.

[9] In der üblichen Form der DCG werden terminale Symbole in eckige Klammern [ ] gesetzt, z.B. N → [boy]. Diese Klammern werden in Prolog zur Kennzeichnung von Listen verwendet und terminale Symbole sind einelementige Listen.