Kapitel 7. Grundbegriffe der Graphentheorie

Im anschaulichen Sinne sind Graphen Darstellungen wie die Abbildungen auf den vorangehenden Seiten. Diese Abbildungen stellen die Struktur von Systemen dar. Im mathematischen Sinn ist ein Graph jedoch die durch eine zweistellige Relation definierte Struktur eines Systems, die geometrische Darstellung also nur eine Abbildung eines solchen Systems.

Definition 7.1. Graph

Ein Graph besteht aus einer Menge M und einer in M definierten zweistelligen Relation R:
=<M, R> mit R ⊆ M×M

Beispiel:

M ={A,B,C,D}
R = {<A, B>, <A, C>, <D, C>}

Definition 7.2. Knoten

Ist = <M, R> ein Graph, dann nennt man die Elemente von M Knoten des .

In unserem Beispiel sind die Knoten des Graphen die Elemente A, B, C und D.

Definition 7.3. Kanten 

Ist = <M, R> ein Graph, dann nennt man ein Element aus R eine gerichtete Kante von .

Die gerichteten Kanten in unserem Beispiel sind also die Paare < A, B>, <A, C> und < D, C>

Ein Graph in diesem abstrakten Sinne kann durch Abbildungen verschiedener Art anschaulich gemacht werden. So kann man z.B. die Elemente von M×M durch ein Gitter von Kreisen und die Elemente von R durch Kennzeichnung der entsprechenden Gitterkreise darstellen.

Abb.7.1.

Beispiel:

M ={ A,B,C,D,E}
R ={  < A,A>,<A,C>,<A,D>,< A,E>,<B,C>,
         <C,A>,<C,B>,< C,C>,<C,D>,< C,E>,
         <D,C>,<E,A>, < E,B>,<E,C>, <E,E> }

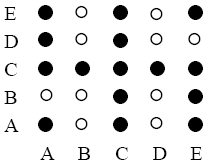
Abb. 7.2.

Aufgabe:

Stellen Sie den Graphen = <M, R>  
M =  {1, 2, 3, 4, 5}    
R = {<1,1>,<2,2>,<3,3>,<4,4>,<5,5>} 
als Gitter dar.

In ähnlicher Weise kann man die Elemente von M×M als ein Netz von Quadraten darstellen, in dem die Elemente von R besonders gekennzeichnet werden.

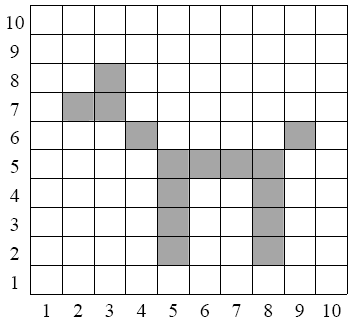
Abb. 7.3. Graph als Gitter

Aufgabe:

Wie lautet der Graph, der Abbildung Abb. 7.3. zugrunde liegt?
M =
R =

Am häufigsten werden Graphen jedoch wie in Abb. 7.4. dargestellt. Ist = <M, R> ein Graph, so ordnet man jedem Elemente x_i aus M einen Punkt (Kreis, Quadrat, Dreieck etc.) a_i zu. Man erhält somit eine eineindeutige Abbildung von M auf eine Menge von Punkten (Kreisen, Quadraten, Dreiecken etc.). Jede Kante < x_i, x_j> aus R wird durch einen Pfeil dargestellt, der die den Elementen x_i und x_j zugeordneten Punkte f(x_i) = a_i und f(x_j) = a_j miteinander verbindet. Die so gewonnene Figur ist eine isomorphe Abbildung von . Dabei können die den Knoten von zugeordneten Punkte beliebig auf der Zeichenebene angeordnet werden. Eine besonders übersichtliche Darstellung erhält man allerdings, wenn man die Knoten nach ihrem Grad anordnet:

Definition 7.4. Grad eines Knotens 

Unter dem Grad eines Knotens soll die Anzahl der verschiedenen Kanten verstanden werden, in denen der Knoten als erstes oder zweites Element vorkommt.

In dem der Abb. 7.4. zugrunde liegenden Graphen haben die Knoten folgende Grade:

g(A) = 7, g(B) = 4, g(C) = 9, g(D) = 4, g(E) = 7

Jetzt kann man die Knoten z.B. vom nächsten zum niedrigsten Grad von oben nach unten anordnen.

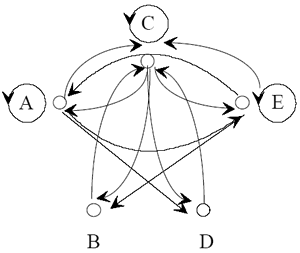
Abb. 7.4.

Graphen haben verschiedene Eigenschaften, die von den Eigenschaften der Relationen abhängen. So ist ein Graph symmetrisch, wenn R symmetrisch ist, asymmetrisch, wenn R asymmetrisch ist, und vollständig, wenn R konnex ist.

Besonders wichtig für die Linguistik sind sog. Bäume.

Definition 7.5. Baum

Ein Graph = <M, R> heißt Baum, wenn er folgende Eigenschaften hat:

• R ist asymmetrisch und intransitiv;
• es gibt genau einen Knoten k, zu dem es keinen Knoten x gibt, so daß < x, k> eine Kante aus R ist; dieser Knoten heißt Wurzel.
• Für beliebige Knoten x, y, z aus M gilt: wenn < x, z> eine Kante ist, dann ist < y, z> keine Kante und umgekehrt.

Bedingung (2) besagt, daß es genau einen Knoten gibt, zu dem keine gerichteten Kanten hinführen. Bedingung (3) garantiert, daß zu allen anderen Knoten eine und nur eine Kante hinführt.

Beispiel:

M = {  A, N, N',V, V',S}
R = { < N',A>,<N',N>,<V',V> ,<S,N'>,=S, V'>}

 

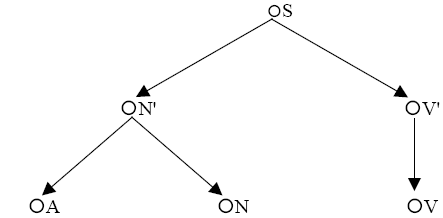
Abb. 7.5.

Jeder Baum enthält Knoten, von denen keine Kanten wegführen. Diese Knoten werden terminale Knoten genannt.

Zu jeder zweistelligen Relation R kann man die konverse Relation R^–1 bilden, indem man die geordneten Paare umdreht. Wenn also <x, y> in R ist, dann ist <y, x> in R⁻¹ und umgekehrt. Man nennt R⁻¹  Konverse von R.

Definition 7.6. Konverse

Eine Relation Q ist Konverse von einer Relation R (geschrieben R⁻¹), wenn gilt:
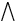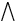xy [R(x,y) ⇒  R⁻¹( y, x)]

Die Konverse von 'x ist Vater von y' ist 'y ist Kind von x' (bzw. 'y hat x zum Vater'). Die Konverse von 'x schlägt y' ist 'y wird von x geschlagen'.

Entsprechend kann man einen zu konversen Graphen ^–1 bilden.

Definition 7.7. Konverse eines Graphen 

Ist = <M, R> ein Graph, dann ist ^–1 = <M, R^–1> die Konverse von .

In der Abbildung eines Graphen wird dabei einfach die Pfeilrichtung umgekehrt. So sieht z.B. der zu Abb. 7.5. konverse Graph wie folgt aus:

 

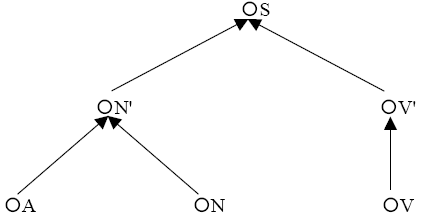
Abb. 7.6.

In der zeichnerischen Darstellung von Baumgraphen kann man die Pfeilspitzen weglassen, wenn man durch Konvention eine Richtung festlegt. Wir wollen dabei die Richtung von oben nach unten festlegen. Abb. 7.6. kann dann wie folgt dargestellt werden:

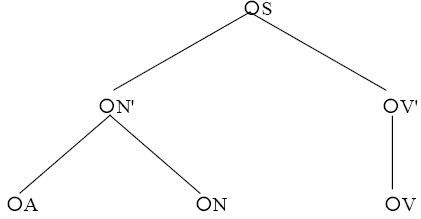
Abb. 7.7.

Wir wollen den zu einem Baum konversen Graphen ebenfalls Baum nennen, wenn keine Mißverständnisse möglich sind. Nach unserer Konvention müßte dann Abb. 7.7. wie in Abb. 7.8. dargestellt werden:

 

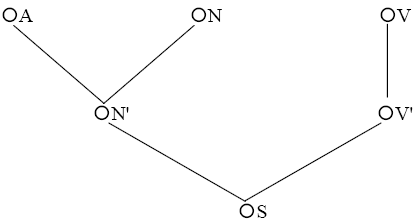
Abb.7.8.

Sind in einer Menge M mehrere Relationen R₁, R₂, …, R_n definiert, so kann man die jeweiligen Graphen ₁ = <M, R₁>, ₂ = <M, R₂>, …, _n = <M, R_n> zu einem Graphen  =  <M, {R₁, R₂, …, R_n}> zusammenfassen.

In der konkreten Repräsentation eines solchen zusammengesetzten Graphen müssen dann allerdings die verschiedenen Relationen durch verschiedene zeichnerische Konventionen unterschieden werden.

Sei z.B. der der Abb. 7.7. zugrunde liegende Graph gegeben und außerdem der Graph ' mit
R' = {<N',V'>,<A,N>,<N,V>}  
dann kann der zusammengesetzte Graph wie folgt dargestellt werden:

 

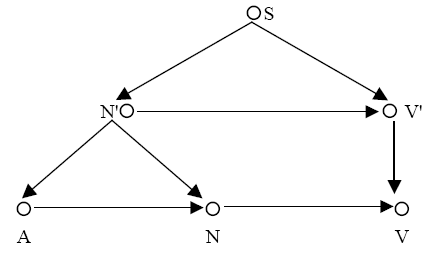
Abb. 7.9.

Auch hier kann eine Konvention festgelegt werden, indem man z.B. bestimmt, daß die zusätzlichen Kanten von links nach rechts angeordnet werden. Die entsprechende Darstellung ist dann mit Abb. 7.7. identisch.

Literatur