Grundbegriffe der Aussagenlogik

3.1. Vorbemerkung

Die Aussagenlogik ist ein Zweig der formalen Logik, der die Beziehungen zwischen Aussagen und Aussagenverbindungen untersucht. Aussagen sind abstrakte Begriffe, auch Propositionen genannt, die in der Alltagssprache durch Sätze ausgedrückt werden. Dabei kommt es in der Aussagenlogik nicht auf den konkreten Inhalt der Aussagen an, sondern nur auf die Entscheidung, ob eine Aussage wahr oder falsch ist. Die Sätze

(3.1.)

a. Der Mars ist ein Planet. b. Der Mond ist ein Planet.

drücken zwei verschiedene Aussagen aus, wovon die erste wahr und die zweite falsch ist. Der Satz

(3.2.) Peter liebt Maria, aber sie verabscheut ihn.

drückt ebenfalls eine Aussage aus. Sie ist jedoch aus zwei einfacheren Aussagen zusammengesetzt, die durch die Sätze

(3.3.)

a. Peter liebt Maria. b. Maria verabscheut Peter.

wiedergegeben werden können. Man nennt solche komplexen Aussagen Aussagenverbindungen. Die Verknüpfung geschieht hier alltagsprachlich durch das Wort aber (in der Bedeutung 'und'). Dabei wird angenommen, daß die Wahrheit der Aussagenverbindung sich aus der Wahrheit der elementaren Aussagen “berechnen” läßt.^[1]

In der formalen Logik werden Aussagen und Aussagenverbindungen durch eine formale Sprache ausgedrückt. Wie bei natürlichen Sprachen unterscheidet man auch bei formalen Sprachen zwischen der Syntax und der Semantik von Ausdrücken. Die Syntax einer Sprache legt durch Regeln fest, wie die Ausdrücke der Sprache gebildet werden können. Die Semantik legt die Bedeutung oder Funktion der Ausdrücke fest.

Die Sprache der Aussagenlogik ist sowohl hinsichtlich ihrer Syntax als auch ihrer Semantik eine sehr einfache Sprache. Sie bildet jedoch die Grundlage für die sehr viel ausdrucksfähigere und für die Linguistik bedeutsamere Prädikatenlogik, die im nächsten Kapitel behandelt wird. Von daher ist es wichtig, die Grundlagen der Aussagenlogik zu kennen.

3.2. Syntaktische Regeln

Wir können die Aussagenlogik zunächst als ein Kalkül in dem in Kapitel 2. definierten Sinne auffassen. Ausgehend von einem Inventar von Grundelementen (dem Vokabular) ist durch Regeln genau festzulegen, welche der aus den Grundelementen bildbaren Zeichenketten zulässig oder ‘wohlgeformt’ sind und welche nicht.

Das Vokabular des Aussagenkalküls besteht aus folgenden Elementen:

1. Aussagenvariable: p, q, r, s, t …
2. Logische Konstante: ∧, ∨, ¬, ⇒^[2]
3. Hilfssymbole: '(', ')', '[', ']', '{', '}'

Die Regeln, die festlegen, welche Zeichenketten wohlgeformte Ausdrücke des Systems sind (Formationsregeln), müssen z.B. bestimmen, daß die Kette (p ⇒ q) ein wohlgeformter Ausdruck ist, während die Kette *(∧ p) q ∨) kein wohlgeformter Ausdruck ist.

Definition 3.1. Formel

Ein wohlgeformter Ausdruck ist eine Formel.

Formationsregeln

Für die Bestimmung der Formeln des Aussagenkalküls sind die folgenden einfachen Formationsregeln ausreichend:

Regel 1:	eine Aussagenvariable ist eine Formel.
Regel 2:	ist P eine Formel, dann ist auch ¬P eine Formel.
Regel 3:	sind P und Q Formeln, dann sind a. (P ∧ Q) b. (P ∨ Q) c. (P ⇒ Q) ebenfalls Formeln.
Regel 4:	Ein Ausdruck ist nur dann eine Formel, wenn er durch Anwendung der oben­stehenden Regeln konstruiert werden kann.

Ableitungsbeispiel:

(1)	p	Regel 1
(2)	q	Regel 1
(3)	¬q	Regel 2, (2)
(4)	(p ∧ q)	Regel 3a, (1), (2)
(5)	¬(p ∧ q)	Regel 2, (4)
(6)	(q ∨¬q)	Regel 3b, (2), (3)
(7)	(¬(p ∧ q) ⇒ (q∨¬q))	Regel 3c, (5), (6)

Die Klammern um die Ausdrücke sind wichtig, weil durch sie die Reihenfolge der semantischen Auswertung geregelt wird. (Mehr dazu weiter unten). Dies läßt sich verdeutlichen, wenn man die Ausdrücke durch Syntaxbäume darstellt.

(3.4.) Syntaxbaum für den Ausdruck (¬(p ∧ q) ⇒ (q∨¬q))

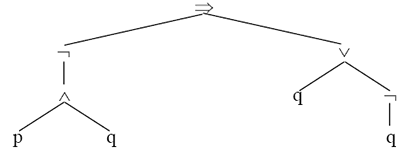
Ähnlich wie in der elementaren Arithmetik, wo Konventionen wie “Punktrechnung geht vor Strichrechnung” gelten, so daß z.B. ein Ausdruck wie 2×3 + 4 als (2×3) + 4 zu lesen ist und somit 2×3 zuerst berechnet werden muß, hat man auch für die logischen Konstanten der Aussagenlogik verschiedene Auswertungsprioritäten festgelegt, welche die Reihenfolge der Auswertung regeln, wenn diese nicht durch Klammern explizit ausgedrückt ist. So ist z.B. der Ausdruck a ∧ b ∨ c als (a ∧ b) ∨ c zu lesen. Man sagt, der Operator ∧ 'bindet' stärker als der Operator ∨.

Es gelten folgende Bindungsregeln:

• ¬ bindet stärker als ∧
• ∧ bindet stärker als ∨
• ∨ bindet stärker als ⇒

Berücksicht man diese Bindungsregeln, kann man die Klammerausdrücke vereinfachen. Die äußerste Klammer kann in jedem Falle weggelassen werden, d.h. (P) vereinfacht sich zu P. Zeile (7) der obigen Ableitung vereinfacht sich dadurch zu ¬(p ∧ q) ⇒ q ∨ ¬q.

3.3. Semantische Regeln

Das durch die Formationsregeln definierte formale System kann mit einer Semantik verbunden werden, durch die jeder Formel ein Wert zugewiesen wird, und zwar nach folgenden Regeln (P und Q sind jeweils Formeln):^[3]

Regel 1:	eine Variable kann die Werte 1 und 0 annehmen
Regel 2:	f(P ∧ Q) =	1, gdw f(P) = 1 und f(Q) =1 0, sonst
Regel 3:	f(P ∨ Q) =	0, gdw f(P) = 0 und f(Q) = 0 1, sonst
Regel 4:	f(P ⇒ Q) =	0, gdw f(P) = 1 und f(Q) = 0 1, sonst
Regel 5a:	f(¬P) =	0, gdw f(P) = 1
Regel 5b:	f( ¬P) =	1, gdw f(P) = 0

Diese Regeln können als eine Charakterisierung der ‘Bedeutung’ der logischen Konstanten aufgefaßt werden, d.h. Regel 2 definiert die Bedeutung der Konstanten ∧, Regel 3 die der Konstante ∨, etc.

Der Wert einer beliebigen Formel kann nun aus den Werten ihrer Konstituenten abgeleitet werden. Im folgenden Ausdruck soll gelten: p = 1 und q = 0:

	¬	(p	∧	q)	⇒	(q	∨	¬	q)
	1	1	0	0	1	0	1	1	0
Schritte:	8	1	5	2	9	3	7	6	4

Auf diese Weise können die Werte des Ausdrucks für alle möglichen Kombinationen der Werte von p und q berechnet werden:

	¬	(p	∧	q)	⇒	(q	∨	¬	q)
	0	1	1	1	1	1	1	0	1
	1	1	0	0	1	0	1	1	0
	1	0	0	1	1	1	1	0	1
	1	0	0	0	1	0	1	1	0
Schritte:	8	1	5	2	9	3	7	6	4

3.4. Interpretation des Aussagenkalküls

Das obige formale System kann auf unterschiedliche Weise interpretiert werden. Im folgenden handelt es sich um das Aussagenkalkül, wenn wir die Variable als Aussagen (Propositionen) auffassen. Der Begriff Aussage ist nicht leicht zu definieren und Gegenstand kontroverser Auseinandersetzungen in der Philosophie. Es möge folgende Arbeitsdefinition gelten:

Definition 3.2. Aussage

Eine Aussage ist das, was durch einen Aussagesatz ausgedrückt wird, wenn wir damit eine Feststellung über einen Sachverhalt treffen.

Ein Ausdruck bezeichnet eine Aussage nur dann, wenn er als wahr oder falsch interpretiert werden kann. Der Satz London ist die Hauptstadt von Uganda z.B. drückt eine Aussage aus, die falsch ist. Zwei oder mehrere Aussagen können durch Ausdrücke, die bedeutungsmäßig etwa den Wörtern 'nicht', 'und', 'oder', 'wenn … dann' entsprechen zu komplexen Aussagen (Aussagenverbindungen) verknüpft werden. Diese Ausdrücke heißen logische Konstante, Funktoren, Junktoren oder Operatoren. Wir können beispiels­weise die obige Aussage und die durch den Satz London ist die Hauptstadt des Vereinigten Königreichs zur Aussagenverbindung London ist die Hauptstadt von Uganda oder London ist die Hauptstadt des Vereinigten Königreichs verknüpfen.

Allgemein gilt, wenn p und q zwei Aussagen sind, dann ist die Verknüpfung p ∨ q ebenfalls eine Aussage, wobei das Zeichen ∨ die logische Konstante 'oder' symbolisiert.

In der Alltagssprache werden Aussagen durch Sätze ausgedrückt. Ein und dieselbe Aussage kann dabei durch verschiedene Sätze ausgedrückt werden. So geben z.B. die folgenden Sätze die gleiche Aussage wieder:

(3.5.)

(a) Sterben ist menschlich (b) Jeder Mensch muß sterben (c) Der Mensch ist sterblich

In loser Redeweise nennt man Sätze Aussagen, wenn sie Aussagen ausdrücken.

Beispiele von Aussagen sind:

(3.6.)

(a) München liegt am Rhein (b) 3 ist eine Primzahl (c) Die Schlange ist ein Vogel (d) Die Luft ist leichter als Wasser

Keine Aussagen sind:

(3.7.)

(a) Ein Objekt ist schwer (b) Rot ist besser als gelb (c) Scher dich zum Teufel

Das Aussagenkalkül ist eine mögliche konkrete Interpretation des obigen formalen Systems, wobei die Variablen Aussagen und die Formeln Aussagenverbindungen repräsentieren. Die Werte stehen für die Wahrheitswerte wahr = 1 und falsch = 0. Die obigen semantischen Regeln definieren die wahrheitsfunktionalen Eigenschaften der logischen Konstanten:

Negation:	¬P	Es ist nicht der Fall daß P, wobei ¬P falsch ist wenn P wahr ist, und wahr, wenn P falsch ist
Konjunktion:	P ∧ Q:	Sowohl P als auch Q, wobei P ∧ Q wahr ist gdw sowohl P als auch Q wahr sind; andernfalls ist es falsch.
Disjunktion:	P ∨ Q:	Entweder P oder Q, oder beides, wobei P ∨ Q falsch ist gdw sowohl P als auch Q falsch ist; andernfalls ist es wahr.
Implikation:	P ⇒ Q:	Wenn P dann Q, wobei P ⇒ Q falsch ist gdw P wahr ist und Q falsch; andernfalls ist es wahr.

3.5. Aussagenverbindungen

Aussagenverbindungen sind Verknüpfungen von Aussagen zu komplexen Aussagen. Verknüpfungen von Aussagen sind Aussagenverbindungen nur dann, wenn sie einen Wahrheits­wert haben, d.h. entweder wahr oder falsch sind. Demnach sind Aussagen­verbindungen selbst Aussagen.

Die Verknüpfung erfolgt durch aussagenlogische Funktoren, denen in der Alltagssprache die Wörter und, oder, wenn … dann entsprechen. Dabei ist jedoch zu berücksichtigen, daß die alltagssprachlichen Wörter nicht eindeutig sind. So hat oder mindestens zwei Bedeutungen:

(a) entweder … oder, oder beides (inklusives oder)

(b) entweder … oder, aber nicht beides (exklusives oder)

Die sprachlichen Mittel einer Wissenschaftsprache müssen jedoch präzise sein. Sie müssen daher genau definiert werden. Dabei entspricht die aussagenlogische Bedeutung nicht immer der alltagssprachlichen. Das ist besonders deutlich bei der sogenannten Implikation (s.u.).

3.5.1. Konjunktion

Aussagenlogische Funktoren werden durch Wahrheitswerte definiert; es sind Aussagen­funktionen. Es wird dabei genau festgelegt, wie der Wahrheitswert einer bestimmten Aussagenverbindung von den Wahrheitswerten der Einzelaussagen abhängt. Da es dabei auf den konkreten Inhalt der Aussagen nicht ankommen soll, ersetzt man die Aussagen durch Aussagenvariable, die durch kleine Buchstaben (p, q, r…) bezeichnet werden.

Die logische Konjunktion zweier Aussagen entspricht ungefähr der Verwendung von und.^[4] 

Der Funktor wird durch das Zeichen ∧ symbolisiert. Sind p und q zwei Aussagen, so ist auch p ∧ q eine Aussage, und zwar mit folgenden Eigenschaften:

Definition 3.3. Konjunktion

Sind P und Q zwei Aussagen, dann ist die Konjunktion P ∧ Q eine wahre Aussage genau dann, wenn sowohl P als auch Q wahr ist. Andernfalls ist sie falsch. Dem entspricht folgende Wahrheitstabelle:

P	Q	P  ∧ Q
w	w	w
w	f	f
f	w	f
f	f	f

Diese Definition der Konjunktion leuchtet unmittelbar ein. Die Aussagenverbindung

(3.8.) München liegt an der Isar, und Bonn liegt an der Weser

ist wahr, wenn München wirklich an der Isar und Bonn wirklich an der Weser liegt. Da Bonn nicht an der Weser liegt, ist diese Aussagenverbindung falsch.

Da es auf den konkreten Inhalt von Aussagen nicht ankommen soll, sondern nur auf den Wahrheitswert, ist auch der folgende Satz aussagenlogisch gesehen, der Ausdruck einer sinnvolle Aussagenverbindung:

(3.9.) Die Katze ist ein Säugetier und 2 + 2 = 4

Es ist sogar eine wahre Aussagenverbindung, da die beiden Einzelaussagen ebenfalls wahr sind.

3.5.2. Disjunktion

Die logische Disjunktion zweier Aussagen entspricht der Verwendung von oder in der Bedeutung 'entweder — oder, oder beides'. Der Funktor wird durch das Zeichen ∨ symbolisiert. Sind P und Q zwei Aussagen, dann ist auch P ∨ Q eine Aussage, und zwar mit folgenden Eigenschaften:

Definition 3.4. Diskunktion

Sind P und Q zwei Aussagen, dann ist die Disjunktion P ∨ Q eine falsche Aussage genau dann, wenn sowohl P als auch Q falsch sind. Andernfalls ist sie wahr. Wahrheitstabelle:

P	Q	P ∨ Q
w	w	w
w	f	w
f	w	w
f	f	f

3.5.3. Konditional

Das Konditional (auch Implikation genannt) hat Ähnlichkeit mit der alltagssprachlichen Verwendung von wenn … dann, sie ist jedoch nicht damit identisch. In der allgemeinen Verwendung bezeichnet die wenn dann-Beziehung auch einen Kausalzusammenhang oder eine notwendige Folge:

(3.10.) Wenn es regnet, wird die Straße naß (Kausalbezeichnung)

(3.11.) Wenn ein Dreieck gleichwinklig ist, ist es auch gleichseitig (notwendige Folge)

Das Konditional meint weder einen Kausalzusammenhang noch eine notwendige Folgerung. Der Funktor für das Konditionel wird durch das Zeichen ⇒ symbolisiert.

Wenn P und Q zwei Aussagen sind, dann ist auch P ⇒ Q (lies: P impliziert Q) eine Aussage, und zwar mit folgenden Eigenschaften:

Definition 3.5. Konditional

Sind P und Q zwei Aussagen, dann ist die Aussagenverbindung P  ⇒ Q eine falsche Aussage genau dann, wenn P wahr und Q falsch ist. Andernfalls ist sie wahr.

P	Q	K ⇒ Q
w	w	w
w	f	f
f	w	w
f	f	w

Diese Definition des Konditionals bereitet Verständnisschwierigkeiten, die z.T. daher rühren, daß die umgangssprachliche Verwendung des Konditionals vom Inhalt der Einzelaussagen abhängig ist. So behauptet die Definition, daß P ⇒ Q auch dann wahr ist, wenn P falsch ist. Beispiel:

(3.12.) Wenn Peter Maria liebt, dann liebt Maria Peter

Man wird zugeben, daß diese Aussage wahr ist, wenn sowohl Peter Maria als auch Maria Peter liebt. Es leuchtet auch ein, daß die Aussage falsch ist, wenn zwar Peter Maria liebt, das umgekehrt aber nicht der Fall ist. Nach der Definition soll die Aussage aber wahr sein, wenn Peter Maria nicht liebt, gleichgültig, ob Maria Peter liebt oder nicht. Das will nicht mehr so recht einleuchten.

Daß diese Definition des Konditionals dennoch sinnvoll ist, zeigt sich im Gesamtsystem der Aussagenlogik. Sie ist für die Schlußregeln notwendig und führt zu keinen Widersprüchen.

3.5.4. Negation

Die logische Negation ist keine Aussagenverbindung im eigentlichen Sinn. Ist p eine Aussage, so ist die Negation von p die Aussage "es ist nicht der Fall, daß p". Der Ausdruck "es ist nicht der Fall, daß" wird durch das Zeichen ¬ symbolisiert.

Ist P eine Aussage, so ist auch ¬P eine Aussage, und zwar mit folgenden Eigenschaften:

Definition 3.6. Negation

Ist P eine Aussage, dann ist die Negation ¬P wahr, wenn P falsch ist, und falsch, wenn P wahr ist.

Wahrheitstafel:

P	¬P
w	f
f	w

Diese Definition leuchtet unmittelbar ein.

3.5.5. Komplexe Aussagenverbindungen

Natürlich gibt es auch Aussagenverbindungen, die aus mehr als zwei Aussagen bestehen. Man kann sie sich aus Aussagen und einfachen Aussagenverbindungen zusammengesetzt denken. Wir haben z.B. formuliert: wenn p und q Aussagen sind, dann ist auch p ⇒ q eine Aussage. Eine Aussagenverbindung ist eine Aussage. Man hat damit gleich eine Bildungsregel für komplexe Aussagenverbindung. p ⇒ q bleibt eine Aussage, auch wenn man p oder q durch beliebige Aussagenverbindungen ersetzt. Um den Bezug der Funktoren eindeutig zu machen, müssen die substituierten Aussagenverbindung eingeklammert werden. Ersetzt man z.B. q durch q  ∨ r, erhält man die komplexe Aussagenverbindung p ⇒ (q ∨ r). Es gibt jedoch bestimmte Konventionen für die Bindekraft der Funktoren (s.o.) ¬ —- ∧ — ∨ — ⇒, ¬ bindet am stärksten, ⇒ am schwächsten. Unter dieser Voraussetzung kann der Ausdruck auch als p ⇒ q ∨ r geschrieben werden.

Für komplexe Aussagenverbindungen gelten somit die gleichen Wahrheitsbedingungen wie für einfache Aussagenverbindungen.

Die Aussage p ⇒ (q ∨ r) ist nach der Definition der Implikation nur dann falsch, wenn p wahr ist und q ∨ r falsch. Die Aussage q ∨ r wiederum ist dann falsch, wenn sowohl q als auch r falsch ist. Folglich ist p ⇒ (q ∨ r) genau dann falsch, wenn p wahr ist und q und r falsch.

Durch schrittweise Anwendung der Wahrheitsfunktionen für die einzelnen Funktoren (z.B. mithilfe der Wahrheitstabellen) lassen sich die Wahrheitswerte von komplexen Aussagen­verbindungen berechnen.

	p	⇒	q	∨	r
	w	w	w	w	w
	w	w	w	w	f
	w	w	f	w	w
	w	f	f	f	f
	f	w	w	w	w
	f	w	w	w	f
	f	w	f	w	w
	f	w	f	f	f
Schritte	1	5	2	4	3

3.5.6. Tautologie und Kontradiktion

Eine wesentliche Aufgabe der Aussagenlogik ist die Untersuchung der Wahrheitswerte von komplexen Aussagenverbindungen. Dabei interessieren vor allem zwei Fälle:

1. Aussagenverbindungen, die immer wahr sind, gleichgültig, welchen Wahrheitswert die Einzelaussagen haben; diese Aussagenverbindungen werden tautologisch genannt.
2. Aussagenverbindungen, die immer falsch sind; sie werden kontradiktorisch genannt.

Definition 3.7. Tautologie

Eine Aussagenverbindung ist eine Tautologie, wenn sie unter allen Inter­pretationen wahr ist.

Definition 3.8. Kontradiktion

Eine Aussagenverbindung ist eine Kontradiktion, wenn sie unter allen Interpretationen falsch ist.

Definition 3.9. erfüllbar

Aussagenverbindungen, die weder tautologisch noch kontradiktorisch sind, heißen erfüllbar oder kontingent.

Eine einfache Tautologie ist z.B.

(3.13.)

a. Es ist nicht der Fall, daß Hans dumm ist und nicht dumm ist. b. ¬(p ∧ ¬p)

Dagegen ist der folgende Satz eine Kontradiktion:

(3.14.)

a. Hans ist ehrlich und unehrlich. b. p ∧ ¬p

<

Das ist leicht einzusehen. Eine Konjunktion ist nur wahr, wenn beide Konjunktionsglieder wahr sind. Ist p wahr, dann ist ¬p falsch; ist p falsch, dann ist ¬p wahr. Folglich ist p ∧ ¬p immer falsch und ¬(p ∧ ¬p) immer wahr. Dies wird auch in der expliziten Berechnung mit Wahrheitsfunktionen deutlich:

¬	(p	∧	¬	p)
w	w	f	f	w
w	f	f	w	f

Die Kontradiktion der Form p ∧ ¬p spielt in der Beweisführung der Mathematik eine große Rolle. Das Verfahren besteht darin, daß man das Gegenteil der zu beweisenden Aussage annimmt und zeigt, daß diese Annahme zu einem Widerspruch führt (reduction ad absurdum). Nach dem gleichen Verfahren läßt sich auch beweisen, ob eine Aussagenverbindung eine Tautologie bzw. eine Kontradiktion ist.

Es soll z.B. gezeigt werden, daß die folgende Aussagenverbindung eine Tautologie ist:

(3.15.)

(p⇒ q∧ q⇒ r) ⇒ (p⇒ r) (Wenn gilt 'p impliziert q' und 'q impliziert r', dann gilt auch 'p impliziert r'.)

Man kann den Beweis dadurch antreten, daß man sämtliche Wahrheitswertkombinationen durchrechnet (das wären immerhin acht Fälle). Das entspricht dem wissenschaftlichen Verfahren der Verifikation. Man kann die Behauptung aber auch zu falsifizieren versuchen.

Eine Aussagenverbindung ist tautologisch, wenn sie immer wahr ist. Wir nehmen nun an, daß (p ⇒ q ∧ q  ⇒ r) ⇒ (p ⇒ r) keine Tautologie ist, d.h. daß sie in mindestens einem Fall falsch ist. Nach der Definition der Implikation müßte dann (p ⇒ q ∧ q ⇒ r) wahr und (p ⇒ r) falsch sein.

(3.16.) (p ⇒ q ∧ q ⇒ r) ⇒ (p ⇒ r)

              w         f     f

Nach der Definition der Konjunktion müssen daher p ⇒ q und q ⇒ r beide wahr sein. Außerdem kann p  ⇒ r nur dann falsch sein, wenn p wahr und r falsch ist.

(3.17.) (p ⇒ q ∧ q ⇒ r) ⇒ (p ⇒ r)

         w    w    w    f   w f  f

Wenn r falsch ist, kann q ⇒ r nur wahr sein, wenn auch q falsch ist. Wenn q falsch ist, kann p ⇒ q nur wahr sein. wenn auch p falsch ist.

(3.18.)(p ⇒ q ∧ q ⇒ r) ⇒ (p ⇒ r)

      F  w f  w f  w  f  f  W  f  f

Die Annahme , daß (p ⇒ q ∧ q ⇒ r) ⇒ (p ⇒ r) keine Tautologie ist, hat die Folge, daß p gleichzeitig wahr und falsch sein müßte. Das ist ein Widerspruch. Folglich ist unsere Annahme falsch und (p ⇒ q ∧ q ⇒ r) ⇒ (p ⇒ r) ist eine Tautologie.

Eine der Hauptaufgaben der formalen Logik ist es zu untersuchen, unter welchen formalen Bedingungen logische Schlüsse gültig sind.

Ein Schluß besteht aus einer Menge von Prämissen, die als wahr angenommen werden und einer Konklusion, die daraus logisch (d.h. unabhängig von der Bedeutung der Prämissen) folgen soll. Ein Schluß ist gültig, wenn es eine entsprechende Aussagenfunktion (Assagenverbindung) gibt, die eine Tautologie ist. Betrachten wir folgendes Beispiel:

Prämissen:	1. Entweder zahlt die Regierung Lösegeld, oder die Terroristen werden ihre Opfer töten
	2. Die Regierung wird jedoch kein Lösegeld zahlen
Konklusion:	Folglich werden die Terroristen ihre Opfer töten.

Die Frage ist nun, ob dieser Schluß gültig ist, d.h. ob die Konklusion tatsächlich logisch aus den Prämissen folgt.

Setzen wir p = Die Regierung zahlt Lösegeld und q = Die Terroristen werden ihre Opfer töten, dann hat die erste Prämisse die Form p ∨ q, die zweite die Form ¬p. Die Konklusion soll aus der Konjunktion der Prämissen folgen, d.h. aus (p ∨ q) ∧ ¬p. Der gesamte Schluß wird also durch die folgende Aussagenverbindung dargestellt:

(3.19.) (p ∨ q) ∧ ¬p ⇒ q

Mithilfe der Wahrheitsfunktionen der Funktoren läßt sich die Gültigkeit dieser Formel berechnen:

Wie die Spalte 8 zeigt ist die Aussagenfunktion unter jeder Interpretation ihrer Variablen wahr und daher eine Tautologie.

Was geschieht nun aber, wenn wir die zweite Prämisse und die Konklusion jeweils durch ihre Negation ersetzen, d.h. durch Die Regierung wird Lösegeld zahlen bzw. Die Terroristen werden ihre Opfer nicht töten?

	(p	∨	q)	∧	p	⇒	¬	q
	w	w	w	w	w	f	f	w
	w	w	f	w	w	w	w	f
	f	w	w	f	f	w	f	w
	f	f	f	f	f	w	w	f
Schritte	1	5	2	6	3	8	7	4

Wie die Spalte 8 zeigt, ist dies kein gültiger Schluß.

3.5.7. Logische Äquivalenz

Verschiedene aussagenlogische Ausdrücke (Formeln) können hinsichtlich ihres wahrheits­funktionalen Verhaltens miteinander verglichen werden. Dabei interessieren insbesondere solche Ausdrücke, die unter den gleichen Bedingungen wahr oder falsch sind. Solche Ausdrücke heißen logisch äquivalent.

Definition 3.10. logisch äquivalent

Zwei aussagenlogische Formeln P und Q heißen logisch äquivalent (symbolisch: P ≡ Q) genau dann, wenn sie unter den gleichen Bedingungen wahr oder falsch sind, d.h. wenn sie für jede konsistente Bewertung ihrer Elementar­aussagen stets den gleichen Wahrheitswert haben.

Mit anderen Worten: äquivalente Formeln haben die gleichen Wahrheitstafeln. Die Äquivalenz setzt normalerweise voraus, daß die Formeln aus den gleichen elementaren Aussagen zusammengesetzt sind. Mit konsistenter Bewertung ist gemeint, daß in beiden Formeln einer Elementaraussage nicht verschiedene Wahrheitswerte zugewiesen werden dürfen.

Beispielsweise sind die Ausdrücke ¬(p ∨ q) und ¬p ∧ ¬q logisch äquivalent, d.h. es gilt ¬(p ∨ q) ≡ ¬p ∧ ¬q. Der Nachweis erfolgt durch Berechnung der Wahrheitstafeln.

p	q	p  ∨ q	¬(p  ∨ q)	¬p	¬q	¬ p ∧ ¬ q
w	w	w	f	f	f	f
w	f	w	f	f	w	f
f	w	w	f	w	f	f
f	f	f	w	w	w	w

Daraus ist ersichtlich, daß ¬(p ∨ q) und ¬p ∧ ¬q in der Tat die gleichen Wahrheitstafeln besitzen. Durch diese Äquivalenz wird ein systematischer Zusammenhang zwischen Negation, Konjunktion und Disjunktion hergestellt, wenn man noch berücksichtigt, daß P und ¬¬P (= ¬(¬P))äquivalente Ausdrücke sind.

Die Äquivalenz von Ausdrücken ist ein ganz entscheidendes Mittel, um systematische formale Zusammenhänge zwischen logischen Ausdrücken darzustellen. Da äquivalente Aus­drücke die gleichen Wahrheitstafeln haben, können Teilausdrücke einer komplexen Formel durch beliebige äquivalente Ausdrücke ersetzt werden, ohne daß sich der Wahrheits­wert des Gesamtausdrucks ändert. Auf diese Weise können dann Äquivalenzen zwischen Ausdrücken durch rein formale, syntaktische Operationen aufgezeigt werden. Mit

1. ¬(P ∨ Q) ≡ ¬P ∧ ¬Q
2. P 𠪪P

läßt sich die Konjunktion durch die Disjunktion und umgekehrt die Disjunktion durch die Konjunktion ersetzen.

1. ¬(p ∧ q)
2. ¬(¬¬p ∧ ¬¬q) mit {p/¬¬p, q/¬¬q}
3. ¬(¬(¬p ∨ ¬q)) mit ¬(P ∨ Q) ≡ ¬P ∧ ¬Q, wenn P = ¬p und Q = ¬q
4. ¬p ∨ ¬ q, wegen P ≡ ¬¬P, wenn P = ¬p ∨ ¬q

Damit ist auch gezeigt, daß ¬(P ∧ Q) ≡ ¬P ∨ ¬ Q, und zwar auf rein syntaktischem Weg, ohne die Wahrheitswerte einzeln zu prüfen.

Die beiden Äquivalenzen

(3.20.) (a) ¬(P ∨ Q) ≡ ¬P ∧ ¬Q und
(b) ¬(P ∧ Q) ≡ ¬P ∨ ¬Q

die mithilfe der Negation einen systematischen Zusammenhang zwischen der Konjunktion und der Disjunktion herstellen, sind als die Gesetze von De Morgan bekannt.

Äquivalenzen zwischen Ausdrücken lassen sich auch per Definition einführen, wobei jedoch gleichzeitig zusätzliche syntaktische Mittel eingeführt werden. Man betrachte beispielsweise den Fall der wechselseitigen Implikation Wenn p dann q, und wenn q dann p: p ⇒ q ∧ q ⇒ p. Diese Formel hat folgende Wahrheitswerte:

p	⇒	q	∧	q	⇒	p
w	w	w	w	w	w	w
w	f	f	f	f	w	w
f	w	w	f	w	f	f
f	w	f	w	f	w	f

Sie hat eine besondere Eigenschaft insofern sie genau dann wahr ist, wenn die elementaren Teilaussagen jeweils den gleichen Wahrheitswert aufweisen. Es ist daher sinnvoll, sie als eigenständige Wahrheitsfunktion zu betrachten und durch einen eigenen Funktor ⇔ zu bezeichnen. Die Funktion P ⇔  Q wird Bikonditional aber auch Äquivalenz genannt.^[5]

Definition 3.11. Bikonditional (Äquivalenz)

Das Bikonditional (die Äquivalenz) ist definiert durch:
P ⇔ Q :⇔ P ⇒ Q ∧ Q ⇒ P
Sind P und Q logische Formeln, so ist das Bikonditional P ⇔ Q eine wahre Aussage, wenn P und Q den gleichen Wahrheitswert haben, andernfalls ist es eine falsche Aussage.

Dem entspricht folgende Wahrheitstabelle:

P	Q	P ⇔ Q
w	w	w
w	f	f
f	w	f
f	f	w

Deutsche Ausdrücke, die dem Bikonditional entsprechen, sind dann und nur dann wenn, genau dann wenn, gerade dann wenn und ist eine notwendige und hinreichende Bedingung für.

Durch derart definitorisch eingeführte Äquivalenzen werden keine neuen Erkenntnisse gewonnen, aber die Ausdrucksfähigkeit der Sprache erweitert.

In ähnlicher Weise ließe sich das Konditional per Definition einführen, wobei gilt P ⇒ Q ≡ ¬P ∨ Q:

P	Q	¬P	¬P  ∨ Q	P  ⇒ Q
w	w	f	w	w
w	f	f	f	f
f	w	w	w	w
f	f	w	w	w

Es wurde schon darauf hingewiesen, daß eine Voraussetzung für die Äquivalenz von Ausdrücken ist, daß sie aus den gleichen Elementaraussagen aufgebaut sind. Beispielsweise können p ∧ q und p ∧ r nicht logisch äquivalent sein. Hingegen sind die Ausdrücke p ∧ (q ∨ ¬q) und p ∧ (r ∨ ¬r) jedoch logisch äquivalent, wie eine Berechnung der Wahr­heitswerte zeigen würde, obwohl sie aus verschiedenen Elementaraussagen gebildet sind. Dies hängt damit zusammen, daß q ∨ ¬q und r ∨ ¬r beides Tautologien sind und somit unabhängig von den Wahrheitswerten von q und r stets genau den gleichen Beitrag für die Berechnung der Wahrheitswerte des Gesamtausdrucks leisten. Wir können allgemein sagen, daß zwei beliebige Tautologien oder zwei beliebige Kontradiktionen logisch äquivalent sind, selbst wenn sie nicht dieselben Elementaraussagen enthalten, da ihre Wahrheitswerte ja unabhängig von diesen Elementaraussagen sind.

Wie bereits ausgeführt sind logisch äquivalente Ausdrücke in der Logik von großer Bedeutung, da sie in jedem Ausdruck beliebig füreinander ersetzt werden können, ohne dessen Wahrheitsgehalt zu ändern. Dadurch wird es möglich, aus Ausdrücken auf rein syntaktischem Wege neue äquivalente Ausdrücke zu bilden.

In der logischen Praxis hat es sich als nützlich erwiesen, ein Grundinventar von logischen Äquivalenzen quasi als Grundgesetze zur Verfügung zu haben, aus denen alle anderen abgeleitet werden können (vgl. Tabelle Abb. 3.3.). Diese Tabelle enthält gewisse Redundanzen, insofern gewisse Äquivalenzen aus anderen abgeleitet werden können.

Idempotenz und Komplementarität

Die Gesetze für die Idempotenz und Komplementarität ergeben sich aus den folgenden Wahrheitstafeln:

P	P  ∧ P	P  ∨ P	¬P	¬¬P	P  ∨  ¬P	P  ∧  ¬P
w	w	w	f	w	w	f
f	f	f	w	f	w	f

P, P ∧ P, P ∨ P, und ¬¬P haben in der Tat die gleichen Wahrheitstafeln und sind somit äquivalent. P ∨ ¬P ist eine Tautologie, was durch P ∨ ¬P ≡ W ausgedrückt wird, hingegen ist P ∧ ¬P eine Kontradiktion: P ∧ ¬P ≡ F.

Die Konjunktion und Disjunktion sind jeweils assoziative Verknpüfungen, d.h. es kommt nicht auf die Reihenfolge der Auswertung an. Da (p ∧ q) ∧ r und p ∧ (q ∧ r) äquivalent sind, können die Klammern auch weggelassen werden: p ∧ q ∧ r.

Kommutativität

Die Gesetze der Kommutativität ergeben sich eigentlich aus der Definition von Konjunktion und Disjunktion:

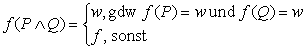
gleichgültig ob man {P/p, Q/q} oder {P/q, Q/p} substituiert.

Distributivgesetz

Das Distributivgesetz 4.a. wird durch die folgenden Wahrheitstafeln verifiziert.

P	Q	R	Q  ∧ R	P  ∨ (Q  ∧ R)	P  ∨  Q	P  ∨ R	(P  ∨  Q)  ∧ (P  ∨ R)
w	w	w	w	w	w	w	w
w	w	f	f	w	w	w	w
w	f	w	f	w	w	w	w
w	f	f	f	w	w	w	w
f	w	w	w	w	w	w	w
f	w	f	f	f	w	w	f
f	f	w	f	f	f	f	f
f	f	f	f	f	f	f	f

 

Gesetze der Identität

Die Gesetze der Identität ergeben sich wiederum aus der Definition von Konjunktion und Disjunktion.

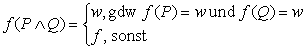
und

 

Für die Konjunktion gilt somit: ist Q eine Kontradiktion (F), so ist die Konjunktion immer falsch, gleichgültig welchen Wert P hat. Ist Q hingeben eine Tautologie (W), so ist der Wahrheitswert der Konjunktion ausschließlich von P abhängig.

Für die Disjunktion gilt: ist Q eine Tautologie (W), so ist die Disjunktion immer wahr, gleichgültig welchen Wert P hat. Ist Q hingegen eine Kontradiktion (F), so ist der Wahrheitswert der Disjunktion ausschließlich von P abhängig.

Gesetze für das Konditional

Das Gesetz 8.a. ist bereits auf S. 28 durch Wahrheitstafeln verifiziert worden. Die übrigen Gesetze lassen sich durch Umformung ableiten, z.B.:

Zeile	Formel	aus Zeile(n)	durch Gesetz
(1)	P⇒ Q
(2)	¬ P∨ Q	(1)	8.a.
(3)	¬ P∨ ¬¬ Q	(2)	6.b. Negation
(4)	¬(P∧ ¬ Q)	(3)	7.b. De Morgan
Folglich:	P⇒ Q≡ ¬(P∧¬ Q)

Zeile	Formel	aus Zeile(n)	durch Gesetz
(1)	P⇒ Q
(2)	¬ P∨ Q	(1)	8.a.
(3)	Q∨ ¬ P	(2)	3.a. Kommutativität
(4)	¬¬ Q∨¬ P)	(3)	6.b. Negation
(5)	¬ Q⇒¬ P	(4)	8.a.
Folglich:	P⇒ Q≡ ¬ Q⇒¬ P

Gesetze für das Bikonditional

Gesetz 9.a. gilt per Definition. Der Beweis von Gesetz 9.b. könnte wie folgt aussehen.

Zeile	Formel	aus	durch Gesetz
(1)	P⇔ Q
(2)	(P⇒ Q)∧(Q⇒ P)	(1)	9.a.
(3)	(¬ P∨ Q)∧(¬ Q∨ P)	(2)	8.a.
(4)	((¬ P∨ Q)∧¬ Q)∨ ((¬ P∨ Q)∧ P)	(3)	4.b. Distributivität
(5)	((¬ P∧¬ Q)∨ (Q∧¬ Q))∨ ((¬ P∧ P)∨ (P∧ Q))	(4)	4.b. Distributivität
(6)	((¬ P∧¬ Q)∨ F)∨ (F∨ (P∧ Q))	(5)	6.c. Komplementarität
(7)	(¬ P∧¬ Q)∨ (P∧ Q)	(6)	5.a. Identität

Wir wollen nun noch einmal auf den Zusammenhang zwischen Äquivalenz und Bikonditional zu sprechen kommen. Wir haben gesagt, daß zwei Aussagen P und Q dann äquivalent sind, wenn sie unter den gleichen Bedingungen wahr oder falsch sind. Das bedeutet aber, daß sie immer nur gleichzeitig wahr oder gleichzeitig falsch sein können: f(P)=f(Q). Aus der Definition des Bikonditionals

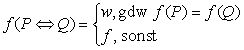
ergibt sich jedoch, daß es genau in diesen Fällen den Wert wahr erhält. Wir kommen damit zu folgendem Theorem:

Theorem 3.1

Für beliebige Aussagen P und Q gilt: P und Q sind logisch äquivalent (P ≡ Q) genau dann, wenn P ⇔ Q eine Tautologie ist.

Zur Illustration soll dies für die Äquivalenz P ⇒ Q ≡ ¬ P ∨ Q demonstriert werden:

P	Q	P  ⇒ Q	¬P	¬P  ∨ Q	(P  ⇒ Q)  ⇔ (¬P  ∨ Q)
w	w	w	f	w	w
w	f	f	f	f	w
f	w	w	w	w	w
f	f	w	w	w	w

Da die Wahrheit einer Tautologie unabhängig von der Wahrheit ihrer Elementaraussagen ist und ausschließlich von der formalen Struktur abhängt, kann man diese Elementaraussagen durch beliebige andere Aussagen ersetzen, ohne daß sich am Status der Tautologie etwas ändert, vorausgesetzt daß die Ersetzung konsistent erfolgt. Ist P ⇔ Q eine Tautologie, so ist auch P'  ⇔ Q' eine Tautologie, wenn P' und Q' durch konsistente Substitution aus P bzw. Q hervorgehen. Wenn man in unserem Beispiel: (p ⇒ q) ⇔ (¬p ∨  q) beispielsweise p durch r ∨ s und q durch ¬s ersetzt, erhält man die Tautologie ((r ∨ s) ⇒ ¬s) ⇔ (¬( r ∨ s) ∨ ¬s) und somit die logische Äquivalenz ((r ∨ s) ⇒ ¬s) ≡ (¬( r ∨ s) ∨ ¬s).

3.6. Logisches Schließen

Die eigentliche Aufgabe der formalen Logik ist es, die Gesetze des logischen Schließens zu untersuchen. Dabei geht es wiederum wesentlich darum zu zeigen, inwieweit die Gültigkeit eines Schlusses sich allein aus seiner Form ergibt.

Definition 3.12. Schluß

Ein Schluß beteht aus einer Menge von Aussagen {P₁,…,P_n}, den Prämissen, die als wahr vorausgesetzt werden, und einer weiteren Aussage K, der Konklusion, deren Wahrheit notwendig aus der Wahrheit der Prämissen folgen soll.

Beispiel:

Prämissen:		Wenn Sokrates ein Mensch ist, so ist er sterblich.
		Sokrates ist ein Mensch
Konklusion:	∴	Sokrates ist sterblich.

Das Zeichen ∴ steht für also und kennzeichnet die Konklusion.

Definition 3.13. Schlußschema

Ein Schlussschema ist eine Schlußform, in der anstelle von Aussagen Aus­sagenvariable stehen.

Ein Schluß ist dann eine Instanz (ein "Einsetzungsbeispiel") eines Schlußschemas, wenn alle Variablen konsistent durch Aussagen ersetzt werden. Unser Beispiel ist eine Instanz des folgenden Schlußschemas, mit den Substitutionen {p/Sokrates ist ein Mensch, q/Sokrates ist sterblich}

(3.21.)     p ⇒ q
    p        
           
∴   q

3.6.1. Logische Implikation

Ein Schluß ist dann gültig, wenn die Konklusion aus den Prämissen logisch folgt. Man nennt die logische Folge Implikation.

Definition 3.14. logische Implikation

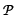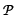
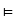Eine Aussage K ist die logische Implikation einer Menge von Aussagen = {P₁,…,P _n} (symbolisch K gdw. P₁ ∧ P₂ ∧ … ∧ P_n ⇒ K eine Tautologie ist.

Definition 3.15. Gültigkeit

Ein Schlußschema aus den Prämissen 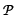 = {P ₁,…,P_n} und der Konklusion K ist gültig gdw. 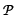K, d.h. wenn das Konditional P₁ ∧ P₂ ∧ … ∧ P_n ⇒ K eine Tautologie ist; andernfalls ist das Schlußschema nicht gültig.

Definition 3.16. gültiger Schluß

Ein Schluß ist gültig, wenn er die Instanz eines gültigen Schlußschemas ist.

Um die Gültigkeit eines Schlußschemas zu beweisen, gilt es also zu zeigen, daß das Konditional aus der Konjunktion der Prämissen und der Konklusion eine Tautologie ist. In unserem Beispiel müßte also gezeigt werden daß (p ⇒ q) ∧ p) ⇒  q tautologisch ist.

Ein sicheres Verfahren, das immer zum Ziel führt, besteht in der Berechnung der Wahrheitswerte:

p	q	p  ⇒ q	(p  ⇒ q)  ∧ p	((p  ⇒ q)  ∧ p)⇒ q
w	w	w	w	w
w	f	f	f	w
f	w	w	f	w
f	f	w	f	w

 

Aufgabe: Es soll überprüft werden, ob der folgende Schluß gültig ist:

(3.22.)     Wenn Hans Meier ein Konservativer ist,
    dann ist er für die Privatisierung der Müllabfuhr
    Hans Meier ist für die Privatisierung der Müllabfuhr
∴   Hans Meier ist ein Konservativer

Dies ist eine Instanz des folgenden Schlußschemas

(3.23.)     p ⇒ q
    q
        
∴   p

Dieses Schema wäre gültig, wenn (p ⇒ q) ∧ q ⇒ p eine Tautologie wäre. Die Wahrheitstabelle dazu lautet:

p	q	p  ⇒ q	(p  ⇒ q)  ∧ q	((p  ⇒ q)  ∧ q)⇒ p
w	w	w	w	w
w	f	f	f	w
f	w	w	w	f
f	f	w	f	w

(p ⇒ q) ∧ q ⇒ p ist nicht tautologisch und das zugrunde liegende Schlußschema somit nicht gültig.

3.6.2. Normalformen

Obwohl die Gültigkeit eines Schlußschemas grundsätzlich immer durch Wahrheitstafeln überprüft werden kann, so ist dies doch oft zu umständlich, insbesondere wenn ein Schlußschema sehr viele verschiedene Aussagenvariable enhält. Für n verschiedene Aus­sagen­variable benötigt man 2ⁿ Zeilen in der Wahrheitstafel. Das folgende Beispiel würde also eine Wahrheitstafel mit 2⁵=32 Zeilen erfordern:

(3.24.)

p ⇒ q p ∨ s q ⇒ r s ⇒ t ∴ t

Im folgenden soll daher ein Verfahren beschrieben werden, das bei mehreren Variablen im allgemeinen schneller zum Ziel führt als die Methode der Wahrheitstafeln und im Gegensatz zum Beweis durch Ableitung (s.u.) mechanisch ausgeführt werden kann. Das Verfahren besteht darin, daß man die zu überprüfenden Formeln durch Äquivalenztransformationen auf wohlbestimmte Normalformen bringt, aus denen man sofort erkennen kann, ob eine Tautologie, eine Kontradiktion oder eine Kontingenz vorliegt. Dabei spielen die folgenden Äquivalenzen eine Rolle:

(3.25.)

(1) p ∨ ¬p ≡ W (2) p ∨ W ≡ W (3) p ∧ ¬p ≡ F (4) p ∧ F ≡ F (5) p ∧ W ≡ p (6) p ∨ F ≡ p

Beispiele für solche Normalformen sind:

(3.26.) (1.a) (p ∨ ¬ p ∨ q) ∧ (¬p& ∨ q ∨ r ∨ ¬r) ∧ (q ∨ ¬q)
(1.b) (p ∨ q ∨ ¬q) ∧ (p ∨ q ∨ r) ∧ (q ∨ ¬p)
(2.a) (p ∧ ¬p) ∨ (q ∧ ¬p ∧ ¬q) ∨ (p ∧ r ∧ ¬r)
(2.b) (p ∧ ¬q) ∨ (q ∧ ¬ ) ∨ (p ∧ ¬p ∧ r)

Dabei sind (1.a) und (1.b) Konjunktionen von Disjunktionen und (2.a) und (2.b) Disjunktionen von Konjunktionen.

Die Formel (1.a) ist eine Tautologie. Die 3 Konjunktionsglieder sind alle tautologisch, weil in jeder Disjunktion ein Teilausdruck der Form P ∨ ¬P (Äquivalenz (1)) vorkommt und damit wegen P ∨ W ≡ W die Disjunktion als ganzes zur Tautologie macht. Die Formel (1.b) hingegen ist keine Tautologie, weil sie kontingente Konjunktionsglieder enthält.

Beispiel (2.a) hingegen ist eine Kontradiktion, da jedes Disjunktionsglied einen Teilausdruck der Form P ∧ ¬P enthält und somit nach Äquivalenz (3) unerfüllbar ist.

Die beiden Formeln (1.a) und (1.b) sind Beispiele für die konjunktive Normalform, die Formeln (2.a) und (2.b) sind Beispiele für die disjunktive Normalform. Wir werden uns im folgenden auf die konjunktive Normalform beschränken.

Definition 3.17. Literal

Ein Literal ist eine Aussagenvariable (positives Literal) oder die Negation einer Aussagenvariable (negatives Literal).

Die Formeln p und ¬p sind Literale.

Definition 3.18. Klausel

Eine Formel ist eine Klausel, wenn sie aus einer Disjunktion von Literalen besteht:
L₁∨ L₂ ∨ … ∨ L_n

Die Formel p ∨ q ∨ ¬r ist eine Klausel, die Formel p ∧ q ∨ ¬r ist keine Klausel.

Definition 3.19. konjunktive Normalform

Eine Formel hat die konjunktive Normalform, wenn sie aus einer Konjunktion von Klauseln besteht.

Beispiele:

1. (p ∨ ¬p) ∧ (q ∨ r ∨ ¬q) mit den Klauseln p ∨ ¬p und q ∨ r ∨ ¬q
2. (¬p ∨ q ∨ r ∨ ¬r) ∧ (q ∨ r) ∧ (¬q ∨ p) mit den Klauseln
   ¬p ∨ q ∨ r ∨ ¬r, q ∨ r und ¬q ∨ p

Theorem 3.2

Eine Formel in der konjunktiven Normalform ist eine Tautologie gdw. in jeder Klausel eine Aussagenvariable als positives und negatives Literal vorkommt.

Beweis: Jede Klausel hat die Form (p ∨ ¬p ∨ Q), wobei Q eine beliebige Disjunktion von Literalen ist. Das ist jedoch eine Tautologie wegen p ∨ ¬p ≡ W und p ∨ W ≡ W. Wir erhalten somit eine Konjunktion von Tautologien, und das ist eine Tautologie.

Jede Formel läßt sich durch Substitution mit Äquivalenzen in die konjunktive Normalform transformieren.

1. Beseitigung des Bikonditionals (Bikond):
   p ⇔ q ≡ (p ⇒ q) ∧ (q ⇒ p)
2. Beseitigung des Konditionals (Kond):
   p ⇒ q ≡ ¬p ∨ q
3. Skopus der Negation verringern (De Morgan):
   ¬(p ∧ q) ≡ ¬p ∨ ¬q
   ¬(p ∨ q) ≡ ¬p ∧ ¬q
4. Doppelte Negation beseitigen (Neg):
   ¬¬p ≡ p
5. Konjunktion nach außen ziehen (Distributivgesetz der Disjunktion: Distrib):
   p ∨ (q ∧ r) ≡ (p ∨ q) ∧ (p ∨ r)
6. Gegebenenfalls Anwendung von Kommutativ- und Assoziativgesetzen (Komm, Assoz):
7. Gegebenenfalls Vereinfachungen (Vereinf):
   a. p ∧ p ≡ p
   b. p ∨ p ≡ p

Beispiel: Es soll gezeigt werden, daß folgendes Schlußschema gültig ist:

(3.27.)    p ∨ q
   ¬p
∴  q

Dies ist dann der Fall, wenn (p ∨ q) ∧ ¬p ⇒ q tautologisch ist:

Formel	Umformung mit
(p ∨ q) ∧ ¬p ⇒ q
¬[(p ∨ q) ∧ ¬p] ∨ q	Kond
[¬(p ∨q)∨ ¬¬p]∨ q	De Morgan
[¬(p ∨ q) ∨ p] ∨ q	Neg
[(¬p ∧ ¬q) ∨ p] ∨ q	De Morgan
[p ∨ (¬p ∧ ¬q)] ∨ q	Komm.
[(p ∨ ¬p) ∧ (p ∨ ¬q)] ∨ q	Distrib.
q ∨[(p ∨ ¬p) ∧ (p ∨ ¬q)]	Komm
[q ∨ (p ∨ ¬p)] ∧ [q ∨ (p ∨ ¬q)]	Distrib
(q ∨ p ∨ ¬p) ∧ (q ∨ p ∨ ¬q)	Assoz

In der ersten Klausel kommen p und ¬p, in der zweiten q und ¬ q vor, folglich ist die Formel tautologisch.

Es soll gezeigt werden, dass die Formel (p ⇒ q) ⇔ ¬p ⇒ ¬q) eine Tautologie ist.

Formel	Umformung mit
(p ⇒ q) ⇔ (¬q ⇒ ¬p)
(¬p ∨ q) ⇔ (¬¬q ∨ ¬p)	Kond
(¬p ∨ q) ⇔ (q ∨ ¬p)	Neg
[(¬p ∨ q) ⇒ (q ∨ ¬p)] ∧ [(q ∨ ¬p) ⇒ (¬p ∨ q)]	Bikond
[¬(¬p ∨ q) ∨ (q ∨ ¬p)] ∧ [¬(q ∨ ¬p) ∨ (¬p ∨ q)]	Kond
[(¬¬p ∧ ¬q) ∨ (q ∨ ¬p)] ∧ [(¬q ∧ ¬¬p) ∨ (¬p ∨ q)]	De Morgan
[(p ∧ ¬q) ∨ (q ∨ ¬p)] ∧ [(¬q ∧ p) ∨ (¬p ∨ q)]	Neg
{[p ∨ (q ∨ ¬p)] ∧ [¬q ∨ (q ∨ ¬p)]} ∧ {[¬q ∨ (¬p ∨ q)] ∧ [p ∨ (¬p ∨ q)]}	Distrib
[(p ∨ q ∨ ¬p) ∧ (¬q ∨ q ∨ ¬p)] ∧ [(¬q ∨ ¬p ∨ q) ∧ (p ∨ ¬p& ∨ q)]	Assoz
(p ∨ q ∨ ¬p) ∧ (¬q ∨ q ∨ ¬p) ∧ (¬q ∨ ¬p ∨ q) ∧ (p ∨ ¬p ∨ q)	Assoz

Die letzte Zeile der Ableitung ist in konjunktiver Normalform. In jeder Klausel kommt eine Aussagenvariable sowohl als positives als auch als negatives Literal vor. Somit haben wir es nach Theorem 3.2 mit einer Tautologie zu tun.

3.6.3. Schlussregeln

Ein weiteres Verfahren, die Gültigkeit eines Schlusses zu beweisen besteht in der Zurück­führung des Schlusses auf eine Kette von gültigen Schlüssen. Jede neue Formel, die aus den Prämissen gültig abgeleitet werden kann, sei es durch eine Äquivalenztransformation, oder als Konklusion eines als gültig erwiesenen Schlußschemas, kann als zusätzliche Prämisse im weiteren Beweisgang verwendet werden.

Ähnlich wie bei den Äquivalenztransformationen ist es nützlich, sich einen Vorrat an gültigen Schlußschemata als Schlußregeln anzulegen.

	Schlußregel		Beispiel
			Modus Ponens (Abtrennungsregel) (M.P)
	p ⇒ q		Wenn Jumbo ein Elefant ist, dann ist er ein Säugetier
	p		Jumbo ist ein Elefant
∴	q	∴	Jumbo ist ein Säugetier
			Modus Tollens (M.T.)
	p ⇒ q		Wenn Jumbo ein Elefant ist, dann ist er ein Säugetier
	¬q		Jumbo ist kein Säugetier
∴	¬p	∴	Jumbo ist kein Elefant
			Kettenregel (K.R.)
	p ⇒ q		Wenn Hans ein Bayer ist, dann ist er ein Deutscher
	q ⇒ r		Wenn Hans ein Deutscher ist, dann ist er ein Europäer
∴	p ⇒ r	∴	Wenn Hans ein Bayer ist, dann ist er ein Europäer
			Resolution (Res.)
	p ∨ q		Der Anlaut ist stimmlos oder der Vokal ist gerundet
	¬p ∨ r		Der Anlaut ist nicht stimmlos oder der Auslaut ist ein Konsonant
∴	q ∨ r	∴	Der Vokal ist gerundet oder der Auslaut ist ein Konsonant
			Modus Tollendo Ponens (M.T.P)
	p ∨ q		Dieser Satz ist ein Aussagesatz oder ein Fragesatz
	¬p		Der Satz ist kein Aussagesatz
∴	q	∴	Der Satz ist ein Fragesatz
			Vereinfachung (V.)
	p ∧ q		[p] ist labial und [k] ist velar
∴	p	∴	[p] ist labial
			Konjunktion (K.)
	p		Hans ist dumm
	q		Fritz ist gescheit
∴	p ∧ q	∴	Hans ist dumm und Fritz ist gescheit
			Addition (Add.)
	p		'der Baum' ist ein Syntagma
∴	p ∨ q	∴	'der Baum' ist ein Syntagma oder 'Baum' ist ein Morphem

Abtrennregel

Die am häufigsten verwendete Schlußregel ist die Abtrennregel mit dem traditionellen Namen modus ponens (genauer modus ponendo ponens) und hat die Form

(3.28.)

p ⇒ q p ∴ q

Die Gültigkeit dieses Schlusses setzt voraus, daß die Formel (p ⇒ q) ∧ p ⇒ q eine Tautologie ist. Dies kann auf verschiedene Weise gezeigt werden.

1. Durch eine Wahrheitstafel

p	q	p ⇒ q	(p ⇒ q) ∧ p	(p ⇒ q) ∧ p ⇒ q
w	w	w	w	w
w	f	f	f	w
f	w	w	f	w
f	f	w	f	w

2. Indirekt durch die Annahme, daß die Formel nicht tautologisch sei, wobei die Berechnung der Wahrheitswerte zu einem Widerspruch führt

(	p	⇒	q	)	∧	p	⇒	q
	w	w	w		w	w	f	f

Die Annahme, daß der Schluß keine Tautologie ist, führt zu dem Widerspruch, daß q gleichzeitig wahr und falsch sein müßte.

3. Durch Vereinfachung mit Äquivalenztransformationen

Schritt	Formel	Äquivalenzregel
(1)	(p ⇒ q) ∧ p ⇒ q)	Konditional (8.a)
(2)	¬[(p⇒ q) ∧ p] ∨ q	De Morgan (7.b)
(3)	[¬(p ⇒ q) ∨ ¬ p] ∨ q	Konditional (8.a)
(4)	[¬(¬ p ∨ q) ∨ ¬ p] ∨ q	De Morgan (7.a)
(5)	[(¬¬ p ∧ ¬ q) ∨ ¬ p] ∨ q	Negation (6.b)
(6)	[(p ∧ ¬ q) ∨ ¬ p] ∨ q	Kommutativität (3.a)
(7)	[¬ p ∨ (p ∧ ¬ q)] ∨ q	Distributivität (4.a)
(8)	[(¬ p ∨ p) ∧(¬ p ∨ ¬ q)] ∨ q	Kommutativität (3.a)
(9)	q ∨ [(¬p ∨ p) ∧ (¬ p ∨ ¬ q) ]	Distributivität (4.a)
(10)	[q ∨ (¬ p ∨ p)] ∧ [q ∨(¬ p ∨ ¬ q)]	Assoziativität
(11)	(q ∨ ¬ p ∨ p) ∧ (q ∨ ¬ p ∨ ¬ q)	Kommutativität
(12)	(q ∨ ¬ p ∨ p) ∧ (¬ p ∨ q ∨¬ q)	Komplementarität (6.a)
(13)	(q ∨ W) ∧ (¬ p ∨ W)	Identität (5.b)
(14)	(q ∨ W) ∧ W	Identität (5.d)
(15)	q ∨ W	Identität (5.b)
(16)	W

4. Überführung in konjunktive Normalform. Das ist fast identisch mit dem vorherigen Verfahren. Zeile (11) ist bereits in KNF.

Modus Tollens

Das Schlußschema des modus tollens (genauer modus tollendo tollens) hat folgende Form (Beispiel s. Tabelle):

(3.29.)

p ⇒ q ¬q ∴ ¬p

Der Beweis erfolgt leicht durch die Äquivalenzregel der Kontraposition (8.c) und der soeben bewiesenen Abtrennregel:

(1)	p ⇒ q	Prämisse
(2)	¬q	Prämisse
(3)	¬q ⇒ ¬p	(1), Kontraposition (8.c)
(4)	¬ p	(2), (3), Abtrennregel

Kettenregel

Die Kettenregel (auch hypothetischer Syllogismus) hat die Form (Beispiel s. Tabelle):

(3.30.)

p ⇒ q q ⇒ r ∴ p ⇒ r

Der Beweis per Wahrheitstafel ist bereits recht umständlich, am einfachsten ist ein indirekter Beweis über Wahrheitswerte:

(	p	⇒	q	)	∧	(	q	⇒	r	)	⇒	(	p	⇒	r	)
	w	w	w		w		f	w	f		f		w	f	f
	5	6	8		3		9	7	4		1		5	2	4

Das Konditional ist nur dann falsch (1), wenn die Konklusion falsch (2) und das Antezedens wahr ist (3). Die Konklusion ist wieder ein Konditional und kann nur falsch sein, wenn das rechte Glied falsch (4) und das Antezedens wahr ist (5). Damit sind die Werte für die Variablen p und r festgelegt. Die Konjunktion (3) kann nur wahr sein, wenn beide Konjunktionsglieder wahr sind (6 u. 7). Ein Konditional (6) mit wahrem Antezendens (5) ist wahr, wenn die Konklusion wahr ist (8). Ein Konditional mit falscher Konklusion ist wahr, wenn das Antezendens falsch ist (9). Das führt zu einem Widerspruch, denn nun müßte q gleichzeitig wahr (8) und falsch sein (9). Damit ist die Annahme, daß die Kettenregel keine Tautologie ist widerlegt.

Resolution

(3.31.)

p ∨ q ¬p ∨ r ∴ q ∨ r

Beweis:

(1)	p ∨ q	Prämisse
(2)	¬p ∨ r	Prämisse
(3)	q ∨ p	(1), Kommutativität
(4)	¬q ⇒ p	(3), Konditional
(5)	p ⇒ r	(2), Konditional
(6)	¬q ⇒ r	(4), (5), Kettenregel
(7)	q ∨ r	(6), Konditional

Wie wir später sehen werden, spielt diese Schlußregel eine wesentliche Rolle im Beweis­verfahren von Prolog, das auschließlich auf Resolution beruht.

Modus Tollendo Ponens

(3.32.)

p ∨ q ¬p ∴ q

Beweis:

(1)	p ∨ q	Prämisse
(2)	¬p	Prämisse
(3)	¬¬p ∨ q	(1), Negation (6.b)
(4)	¬p ⇒ q	(3), Konditional (8.a)
(5)	q	(2), (4), Abtrennregel

Vereinfachung

(3.33.)

p ∧ q ∴ p

Beweis:

(1)	p ∧ q ⇒ p
(2)	¬(p ∧ q) ∨ p	Konditional
(3)	p ∨ ¬(p ∧ q)	Kommutativität
(4)	p ∨ ¬p ∨ ¬q	De Morgan
(5)	W ∨ ¬q	Komplementarität
(6)	¬q ∨ W	Kommutativität
(7)	W	Identität

Konjunktion

(3.34.) p q ∴ p ∧ q

Beweis:

(1)	p ∧ q ⇒ p ∧ q
(2)	¬(p ∧ q) ∨ (p ∧ q)	Konditional
(3)	(p ∧ q) ∨ ¬ (p ∧ q)	Kommutativität
(4)	W	Komplementarität

(p ∧ q) ∨ ¬(p ∧  q) ist eine Instanz von p ∨ ¬p mit der Substitution {p/p ∧ q}

Addition

(3.35.)

p ∴ p ∨ q

Beweis:

(1)	p ⇒ p ∨ q
(2)	¬p ∨ p ∨ q	Konditional
(3)	p ∨ ¬p ∨ q	Kommutativität
(4)	W ∨ q	Komplementarität
(5)	q ∨ W	Kommutativität
(6)	W	Identität

Aufgabe:    Der Butler oder der Koch oder der Chauffeur hat den Baron umgebracht. Wenn der Koch den Baron umgebracht hat, dann war der Eintopf vergiftet, und wenn der Chauffeur den Baron umgebracht hat, dann war eine Bombe im Auto. Der Eintopf war nicht vergiftet und der Butler hat den Baron nicht umgebracht. Also hat der Chauffeur den Baron umgebracht.

Überprüfen Sie die Gültigkeit dieses Schlusses.

Es sei

B = Der Butler hat den Baron umgebracht.

K = Der Koch hat den Baron umgebracht.

C = Der Chauffeur hat den Baron umgebracht.

E = Der Eintopf war vergiftet

b = Es war eine Bombe im Auto

Beweis:

(1)	B ∨ K ∨ C	Prämisse
(2)	(K ⇒ E) ∧ (C ⇒ b)	Prämisse
(3)	¬E ∧ ¬B	Prämisse
(4)	¬B	(3), Vereinf.
(5)	K ∨ C	(1), (4), Modus Tollendo Ponens
(6)	K ⇒ E	(2), Vereinf.
(7)	¬E	(3), Vereinf.
(8)	¬K	(6), (7), Modus Tollens
(9)	C	(5), (8), Modus Tollendo Ponens

3.6.4. Der Konditionalbeweis

Unter bestimmten Umständen können Schlüsse, deren Konklusion ein Konditional als Hauptverknüpfung enthält, mit der Methode des Konditionalbeweises leichter bewiesen werden. Angenommen ein Schluß enthält die Aussagen p, q, r, …, z als Prämissen und m ⇒ n als Konklusion. In einem Konditionalbeweis wird das Antezedens des Konditionals (hier also m) als vorläufige Prämisse hinzugenommen und dann n als Konklusion abgeleitet. Anstatt

(3.36.)

p q r ∶ z ∴ m ⇒ n

zu beweisen, beweisen wir

(3.37.)

p q r ∶ z m ∴ n

Ein Schlußschema ist dann und nur dann gültig, wenn die Implikation mit der der Konjunktion der Prämissen als Antezedens und der Konklusion als Konsequens eine Tautologie ist, in unserem Fall muß das für (p ∧ q ∧ … ∧ z) ⇒ (m ⇒ n) einerseits und (p ∧ q ∧ … ∧ z ∧ m) ⇒ n andererseits gelten. Die Gültigkeit des Konditionalbeweises beruht auf der Tatsache, daß diese beiden Aussagenverbindungen logisch äquivalent sind, wie folgende Ableitung zeigt:

(1)	(p ∧ q ∧ … ∧ z) ⇒ (m ⇒ n)
(2)	¬(p ∧ q ∧ … ∧ z) ∨ (m ⇒ n)	(1) Kond.
(3)	¬(p ∧ q ∧ … ∧ z) ∨ (¬m ∨ n)	(2) Kond.
(4)	(¬(p ∧ q ∧ … ∧ z) ∨ ¬m) ∨ n	(3) Assoz.
(5)	¬((p ∧ q ∧ … ∧ z) ∧ m) ∨ n	(4) DeM.
(6)	((p ∧ q ∧ … ∧ z) ∧ m) ⇒ n	(5) Kond.

Beispiel:

(3.38.)

p ⇒ (q ∨ r) ¬r ∴ p ⇒ q

Beweis:

(1)	p ⇒ (q ∨ r)	Prämisse
(2)	¬r	Prämisse
(3)	p	Konditionalbeweis
(4)	q ∨ r	(1),(3), Modus Ponens
(5)	r ∨ q	(4),Kommutativität
(6)	q	(2),(5), Modus Tollendo Ponens
(7)	p ⇒ q	Konditionalbeweis

3.6.5. Der indirekte Beweis (Reductio ad absurdum)

Die bisherigen Beweisverfahren gehören all zur Klasse der direkten Beweise, die durch eine endliche Folge von gültigen Ableitungsschritten als letzte Zeile einer Ableitung die Konklusion liefern.

Ein besonders in der Mathematik häufig verwendetes Beweisverfahren ist der indirekte Beweis, traditionell auch reductio ad absurdum genannt. Bei einem indirekten Beweis wird die Negation der zu beweisenden Konklusion als vorläufige Prämisse hinzugenommen, und zu zeigen versucht, daß die so entstandene Aussagenmenge zu einem Widerspruch führt. Wenn die einzelnen Ableitungsschritte zulässig sind, dann kommt man zu einem Widerspruch dann, wenn eine oder mehrere Prämissen falsch sind. Da alle ursprünglichen Prämissen als wahr vorausgesetzt werden, muß die als Prämisse hinzugenommene Negation der zu beweisenden Konklusion falsch sein. Somit ist die zu beweisende Konklusion wahr. Betrachten wir dazu folgendes Beispiel:

(3.39.)

p ∨ q q ⇒ r ¬r ∴ p

Bei einem indirekten Beweis geht man folgendermaßen vor:

 

(1)	p ∨ q	Prämisse
(2)	q ⇒ r	Prämisse
(3)	¬r	Prämisse
(4)	¬p	Indirekter Beweis
(5)		q	(1),(4) Modus Tollendo Ponens
(6)		r	(2),(5) Modus Ponens
(7)		r ∧ ¬r	(3),(6) Konjunktion
(8)	p

Zu beweisen ist p. In Zeile (4) wird die Negation ¬p vorläufig zu den Prämissen hinzugenommen. Dies führt in Zeile (7) zu dem Widerspruch r ∧ ¬r. ¬p muß daher falsch sein. Somit ist p wahr.

3.6.6. Das Resolutionsprinzip

Der indirekte Beweis (reductio ad absurdum) hat in den letzten Jahrzehnten in Verbindung mit dem Schlußschema der Resolution und der konjunktiven Normalform in der Forschung zum automatischen Beweisen große Bedeutung erlangt. Dieses sog. Resolutionsprinzip wurde in den sechziger Jahren von J. A. Robinson (s. Robinson 1965) begründet.

Dieses Prinzip beruht wie der Name schon sagt auf dem Schlußschema der Resolution:

(3.40.)

p ∨ q ¬p ∨ r ∴ q ∨ r

Man bezeichnet die Konklusion beim Resolutionsschema als Resolvente.

Der Beweis soll hier der Bequemlichkeit halber noch einmal aufgeführt werden:

(1)	p ∨ q	Prämisse
(2)	¬p ∨ r	Prämisse
(3)	q ∨ p	(1), Kommutativität
(4)	¬q ⇒ p	(3), Konditional
(5)	p ⇒ r	(2), Konditional
(6)	¬q ⇒ r	(4), (5), Kettenregel
(7)	q ∨ r	(6), Konditional

Der Schluß ist jedoch auch intuitiv einsichtig: Ist p wahr, dann muß ¬p falsch sein. Wenn nach Voraussetzung aber ¬p ∨ r wahr sein soll, und ¬p aber falsch ist, dann muß r wahr sein. Ist andererseits aber p falsch, dann muß wenn p ∨ q wahr sein soll, q wahr sein. Nimmt man beide Möglichkeiten zusammen, so ergibt sich q ∨ r.

Man kann das Schlußschema des Modus Tollendo Ponens als Sonderfall der Resolution auffassen:

(3.41.)

p ∨ q ¬p ∴ q

Mit anderen Worten, die Resolution von p ∨ q und ¬p hat als Resolvente q.

(1)	p ∨ q	Prämisse
(2)	¬p	Prämisse
(3)	¬p ∨ F	Addition
(4)	q ∨ F	Resolution
(5)	q	Identität

Ein weiterer Sonderfall ist die Resolution von p und ¬p, die zum Widerspruch führt. Man könnte wie folgt argumentieren:

(1)	p	Prämisse
(2)	¬p	Prämisse
(3)	p ∨ F	Addition
(4)	¬p ∨ F	Addition
(5)	F ∨ F	(3),(4) Resolution
(6)	F	Idempotenz

Man bezeichnet die Resolvente von p und ¬p mit .

Voraussetzung für die fruchtbare Anwendung des Resolutionsschemas ist, daß alle Prämissen Klauselform haben, d.h. Disjunktionen von Literalen sind. Dazu müssen Formeln gegebenenfalls in die konjunktive Normalform übersetzt werden. Die einzelnen Klauseln einer Konjunktion werden zu selbständigen Prämissen (Vereinfachunsschema).

Das Beweisverfahren ist das des indirekten Beweises, d.h. die Negation der zu beweisenden Aussage wird zu den Prämissen hinzugenommen. Es wird dann das Resolutionsschema auf Paare von Aussagen angewandt und die Resolvente zur Aussagenmenge hinzugefügt, solange bis ein Widerspruch entsteht oder die Resolution nicht mehr angewandt werden kann.

Prämissen	Übersetzt in Klauselform
p ∨ q	(1)	p ∨ q
q ⇒ r	(2)	¬q ∨ r
¬r	(3)	¬r
	(4)	¬p	Indirekter Beweis
	(5)	¬q	(2),(3) Resolution
	(6)	p	(1),(5) Resolution
	(7)		(5),(6) Resolution

Das Verfahren zum Beweis einer Aussage p nach dem Resolutionsprinzip auf der Grundlage einer Aussagenmenge 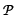kann wie folgt beschrieben werden:

1. Übersetze alle Aussagen aus in Klauselform. Die so erhaltene Klauselmenge sei .
2. Negiere p, übersetze das Resultat in Klauselform und füge das Ergebnis zur Klauselmenge hinzu.
3. Wiederhole die folgenden Schritte solange, bis eine Kontradiktion gefunden ist, oder erkennbar ist, daß kein Ergebnis erzielbar ist.
   1. Wähle zwei Klauseln K₁ und K₂ aus der jeweils gültigen Klauselmenge _n derart, daß es ein Literal L gibt, das in einer der beiden Kauseln positiv, in der anderen negativ vorkommt.
   2. Bilde die Resolvente R aus K₁ und K₂.
   3. Wenn R = , dann ist ein Widerspruch gefunden worden. Andernfalls füge R zur Klauselmenge _n hinzu.

Nehmen wir als weiteres Beispiel die Aufgabe von Seite.

Prämissen	Übersetzt in Klauselform
B ∨ K ∨ C	(1)	B ∨ K ∨ C
(K ⇒ E) ∧ (C ⇒ b)	(2)	¬K ∨ E
	(3)	¬C ∨ b
¬E ∧ ¬B	(4)	¬E
	(5)	¬B
	(6)	¬C	Ind. Bew.
	(7)	K ∨ C	(1),(5)
	(8)	¬K	(2),(4)
	(9)	C	(7),(8)
	(10)		(6),(9) (Kontrad.)

Literatur

Allwood, Jens/Andersson, Lars-Gunnar/Dahl, Östen

1973      Logik für Linguisten. Ins Deutsche übersetzt von Michael Grabski. (= Romanistische Arbeitshefte 8.) Max Niemeyer Verlag: Tübingen.

Genesereth, Michael R. / Nilsson Nils J.

1987      Logical Foundations of Artificial Intelligence. Morgan Kaufmann Publishers: Los Altos, CA.

Heringer, Hans Jürgen

1972      Formale Logik und Grammatik. (= Germanistische Arbeitshefte 6.) Max Niemeyer Verlag: Tübingen.

McCawley James D.

1981      Everything that Linguists have always Wanted to Know about Logic but were ashamed to ask. Basil Blackwell: Oxford.

Partee, Barbara Hall

1978      Fundamentals of Mathematics for Linguistics. D. Reidel Publishing Company: Dordrecht/ London.

Partee, Barbara H./ter Meulen, Alice/Wall, Robert E.

1990      Mathematical Methods in Linguistics. Kluwer Academic Publishers: Dordrecht/ Boston/London. [Entstanden aus Partee (1978) und Wall (1973)]

Robinson, J.A.

1965      A Machine-oriented Logic Based on the Resolution Principle. In: Journal of the Association for Computing Machinery 12, 23--41.

Suppes, Patrick;

1957      Introduction to Logic. D. van Nostrand Company: Princeton, N.J./Toronto/London/New York.

Wall, Robert

1973a     Einführung in die Logik und Mathematik für Linguisten. Band 1: Logik und Mengenlehre. Übersetzt von Wolfgang Klein, Angelika Kratzer und Arnim v. Stechow. Scriptor Verlag: Kronberg, Ts.

1973b     Einführung in die Logik und Mathematik für Linguisten. Band 2: Algebraische Grundlagen. Übersetzt von Wolfgang Klein, Angelika Kratzer und Arnim v. Stechow. Scriptor Verlag: Kronberg, Ts.