Kapitel 5. Grundbegriffe der Mengenlehre

5.1. Warum Mengenlehre?

Rolle von Mengen in der Begriffsentwicklung der Linguistik.

Kategorien: lexikalische und syntaktische

Distribution

Merkmale

Mengen als Alltagsbegriffe.

Naive Mengenlehre

5.2. Menge und Element

Einer der allgemeinsten Begriffe ist der Begriff Menge, die Zusammenfassung von wohlunterschiedenen Objekten (Individuen) zu einem begrifflichen Ganzen. Natürliche Sprachen enthalten zahlreiche Wörter wie Gruppe, Herde, Meute, Rudel, Schar, Schwarm, Mannschaft, die zur Bezeichnung von Mengen in diesem Sinne verwendet werden.

Definition 5.1. Individuum

Bestimmte, wohlunterschiedene Objekte unserer Anschauung oder unseres Denkens nennen wir Individuen.

Individuen nicht notwendigerweise konkret

Definition 5.2. Menge

Unter einer Menge versteht man jede Zusammenfassung von Individuen zu einem Ganzen.

Beispiele für Mengen:

• die Menge der Seminarteilnehmer
• die Menge der natürlichen Zahlen, die kleiner als 10 sind
• die Menge der Beamten, die Radfahrer sind
• die Menge der Wörter der deutschen Sprache
• die Menge der natürlichen Zahlen, die kleiner als 0 sind

Definition 5.3. Element

Die Objekte, die zu einer Menge zusammengefaßt sind, nennt man Elemente der Menge.

Beispiel:

Definition 5.4. Elementbeziehung

Die Elementbeziehung ist eine (zweistellige) logische Beziehung zwischen einem Individuum und der Menge, der das Individuum angehört.

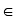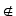Die Elementbeziehung ist Element von wird durch , die Beziehung ist nicht Element von durch symbolisiert.

Es sei M die Menge der natürlichen Zahlen, die größer als 5 sind, dann gilt z.B.:

(5.1.) (a) 7 ist Element von M

(5.2.) (a) 4 ist nicht Element von M

In symbolisierter Sprache schreibt man dafür kürzer:

(5.1.) (b) 7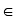M

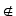(5.2.) (b) 4M

Ein Individuum kann gleichzeitig Element von mehreren Mengen sein. Es gibt einige zusammengesetzte Substantive wie Jagdbomber oder Dichterkomponist, die diese Eigenschaft aufweisen. Wenn jemand ein Dichterkomponist ist, ist er gleichzeitig ein Dichter und ein Komponist.

Die Elemente einer Menge brauchen weder konkret nocht real zu sein. Auch abstrakte oder imaginäre Objekte wie Zahlen, Einhörner, oder der Stein der Weisen können Elemente einer Menge sein. Da Mengen als Ganzheiten betrachtet werden, können die Elemente einer Menge können selbst Mengen sein. Die Bundesliga z.B. ist eine Menge von Elementen, die selbst Mengen sind, die Bundesligamannschaften, die ihrerseits Mengen von Individuen, den einzelnen Spielern, sind.

Mengen können aus endlich oder unendlich vielen Elementen bestehen. Die Menge der Seminarteilnehmer ist endlich, die Menge der natürlichen Zahlen unendlich.

Man kann Mengen auf zwei Arten beschreiben:

1. indem man Ihre Elemente aufzählt
2. durch eine Beschreibung, die auf alle Elemente zutrifft (Aussonderung durch eine Eigenschaft)

Mengen kennzeichnet man durch geschweifte Klammern (Mengenklammern): {  }

Gegeben sei die Menge M der natürlichen Zahlen, die kleiner als 5 sind. In aufzählender Schreibweise ist M beschrieben durch:

(5.3.) {1, 2, 3, 4}

Die Reihenfolge der Nennung der Elemente spielt dabei keine Rolle. Die Mengen (5.3.) und (5.4.) sind identisch:

(5.4.) {2, 3, 1, 4}

Die aufzählende Mengenschreibweise ist nur möglich bei endlichen Mengen und nur praktisch bei kleinen Mengen. Sie ist allerdings notwendig bei Mengen, deren Elemente keine gemeinsame Eigenschaft haben, wie z.B. die Menge {Hut, 3, §}.

Die Menge der natürlichen Zahlen läßt sich nicht durch Aufzählung beschreiben.

Man vergleiche folgende Paraphrasen:

 

Die Ausdrücke (5.5.) (d) und (e) lassen sich in symbolisierte Sprache übersetzen:

1. der Ausdruck Menge der wird durch die Mengenklammer symbolisiert
2. der Ausdruck für die gilt wird durch einen Längsstrich '|' symbolisiert
3. der Ausdruck x hat die Eigenschaft P wird durch den prädikatenlogischen Ausdruck P(x) symbolisiert

Der Ausdruck (5.5.)(d) läßt sich dann wie folgt in symbolisierter Sprache schreiben:

(5.6.)   {x | x ist eine natürliche Zahl}

Bezeichnet man den Ausdruck natürliche Zahl durch das Symbol N, kann man noch kürzer schreiben

(5.7.)   {x | N(x)}

Ausdrücke, mit denen man Mengen bezeichnet, nennt man Mengenzeichen. Die Ausdrücke {..., ..., ...} und {x | P(x)} sind Mengenzeichen. Als allgemeine Mengenzeichen verwendet man Großbuchstaben: A, B, C ..., insbesondere M mit oder ohne Index (M₁, M₂, M_i ...).

Verschiedene Mengenzeichen können die gleiche Menge bezeichnen.

Beispiel:

(5.8.)   (a)        {1, 2} 
           (b)       {x | x ist natürliche Zahl kleiner als 3}

Statt "die durch A bezeichnete Menge" sagt man kurz "die Menge A"

Man kann auch Regeln formulieren, welche die Bedingungen festlegen, die für die Mitgliedschaft in der Menge erfüllt sein müssen. Sei G={2, 4, 6, …} die Menge der geraden natürlichen Zahlen (d.h. G={x | gerade(x)}, dann läßt sich die Mitgliedschaft wie folgt definieren:

1. ist ein Element von G

2. wenn x ein Element von G ist, dann ist auch x+2 in G

3. nur nach 1. oder 2. bildbare Individuen sind Elemente von G

Durch eine unerfüllbare Bedingung wie x<0 ∧ x>1 wird man auf die leere Menge geführt.

Definition 5.5. leere Menge

Die leere Menge oder Nullmenge ist die Menge, die keine Elemente hat. Sie wird üblicherweise durch das Zeichen 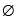bezeichnet, obwohl das Mengenzeichen {  } konsequenter wäre. Es kann nur eine leere Menge geben. Man kann sie durch eine beliebige unerfüllbare Eigenschaft definieren, z.B.:        
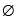:= {x 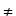| x x}

Ein weiterer Sonderfall einer Menge ist eine Menge mit nur einem Element. Obwohl es Ausdrücke wie Einmannbebtrieb oder Einmannkapelle gibt, besteht in der Alltagssprache die Neigung Einermengen mit dem Objekt, aus dem sie jeweils bestehen, zu identifizieren. Für eine saubere Begriffsbildung ist es jedoch notwendig, die beiden zu unterscheiden. Bob Beamon und die Menge, die Bob Beamon als einziges Element enhält sind nicht die gleichen Objekte. Bis 1991 konnte letztere beispielsweise definiert werden als die Menge aller Leichtathleten, die 8,90m oder weiter gesprungen sind. Bis 1991 traf es sich, daß diese Menge nur Bob Beamon als Element enhielt. Seit den olympischen Spielen von Tokyo 1991 kam mit Mike Powell ein zweites Element hinzu.

Definition 5.6. Einermenge

Eine Einermenge ist eine Menge mit nur einem Element. Ist M eine Menge, dann ist {M} die Einermenge von M.

Sei H={a, b}, dann ist {H}={{a, b}}. Man beachte, daß H  zwei Elemente hat, {H} aber nur eines.

Häufig werden die Bezeichnungen Menge und Klasse mit gleicher Bedeutung verwendet. Es ist jedoch sinnvoll einen Unterschied zu machen und von Klassen nur dann zu sprechen, wenn die Elemente durch gleiche Eigenschaften definiert sind:

Definition 5.7. Klasse

Eine Menge ist eine Klasse, wenn alle ihre Elemente durch gemeinsame Merkmale definiert sind.

Die meisten Mengen, mit denen wir es in der Sprachwissenschaft zu tun haben, sind Klassen in diesem Sinne.

5.3. Beziehungen zwischen Mengen

Man kann Mengen hinsichtlich ihrer Elemente vergleichen und aufgrund gewisser Beziehungen zwischen Mengen neue Mengen bilden.

Definition 5.8. gleich

Zwei Mengen heißen gleich, wenn sie die gleichen Elemente enthalten.         
A = B:⇔ 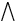x (x ∈ A ⇔ x  ∈ B)

Definition 5.9. disjunkt

Zwei Mengen heißen disjunkt, wenn sie keine gemeinsamen Elemente haben.
disjunkt(A, B) :⇔ ¬x(x ∈ A ∧ x ∈ B)

Definition 5.10. Teilmenge

Eine Menge M₁ ist Teilmenge einer Menge M₂ (ist in M₂ enthalten), wenn jedes Element aus M₁ auch Element aus M₂ ist. Die Beziehung ist enthalten wird durch das Zeichen ⊆ symbolisiert. 
M₁ ⊂ M₂:⇔ x (x ∈ M₁ ⇒ x ∈ M₂)

Beispiel: Die Menge {a, c, e} ist in der Menge {a, b, c, d, e} enthalten.

Nach der Definition der Teilmenge ist auch {a, c, e} in {c, e, a} enthalten. Diese Mengen sind jedoch identisch. Nach dieser Definition ist jede Menge in sich selbst enthalten. Das kommt auch in der Form des Inklusionszeichens ⊆ zum Ausdruck, das man sich aus den Zeichen ⊂ und = zusammengesetzt denken kann.

Es gibt noch einen engeren Begriff der Teilmenge der den Fall der Gleichheit von Mengen ausschließt:

Definition 5.11. Echte Teilmenge

Eine Menge M₁ ist eine echte Teilmenge einer Menge M₂ (ist in M₂ echt enthalten), wenn M₁ eine Teilmenge von M₂ ist, beide Mengen aber verschieden sind: M₁ ≠ M₂.  
M₁ ⊂ M₂ :⇒ M₁ ⊆ M₂ ∧ M₁ ≠ M₂

Zu den Begriffen Teilmenge und echte Teilmenge gibt es die Umkehrbegriffe Obermenge und echte Obermenge:

Definition 5.12. Obermenge

Eine Menge M₁ ist eine Obermenge einer Menge M₂, genau dann, wenn M₂ eine Teilmenge von M₁ ist: 
M₁ ⊆ M₂ :⇒ M₂ ⊆ M₁

Definition 5.13. echte Obermenge

Eine Menge M₁ ist eine echte Obermenge einer Menge M₂, genau dann, wenn M₂ eine echte Teilmenge von M₁ ist:         
M₁ ⊃ M₂ :⇔ M₂ ⊂ M₁

Zwischen ∈ und ⊂ ist streng zu unterscheiden, was in der Alltagssprache häufig nicht beachtet wird. Der Ausdruck ist ein in Hansi ist ein Kaninchen und in Ein Kaninchen ist ein Säugetier bedeutet jeweils etwas anderes: im ersten Falle bezeichnet es die Elementbeziehung (Hansi ∈ Kaninchen) im zweiten die Teilmengenbeziehung (Kaninchen⊂Säugetier).

Mengenbeziehungen können mit Hilfe von sog. Venndiagrammen^[1]  veranschaulicht werden. Dabei muß man sich die Objekte, die zu Mengen zusammengefügt werden, in einer Ebene verteilt denken. Die Elemente einer bestimmten Menge werden durch eine Linie einge­schlossen.

Beispiel:

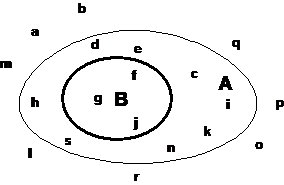
Abb. 5.1.

Durch die dünne Linie wird die Menge A = {c, d, e, f, g, h, i, j, k, n, s}dargestellt, durch die dicke Linie die Menge B ={f, g, j}.

Die graphische Darstellung zeigt deutlich, daß B echte Teilmenge von A ist.

Wenn zwei "Mengenlinien" sich schneiden, entstehen neue geschlossene Linienzüge, d.h. neue Mengen.

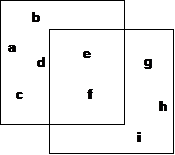
Abb. 5.2.

Außer den Mengen A ={a, b, c, d, e, f} und B ={e, f, g, h, i} sind in Abb. 5.2. noch vier weitere Mengen dargestellt, die sich unter Bezug auf die Mengen A und B definieren lassen.

Abb. 5.3.

In Abb. 5.3. ist die Menge {e, f} herausgehoben. Bezogen auf die Mengen A und B läßt sie sich beschreiben als die Menge der Elemente, die Elemente sowohl aus A also auch aus B sind. Sie wird Schnittmenge von A und B genannt. Die Operation der Schnittbildung wird durch das Zeichen ∩ symbolisiert. Für die Schnittmenge von A und B schreibt man in symbolisierter Sprache

(5.9.)   A ∩ B

Dieser Ausdruck wird gelesen als "A geschnitten mit B".

Definition 5.14. Schnittmenge

Die Schnittmenge zweier Mengen M₁ und M₂ ist die Menge der Elemente, die sowohl zu M₁ als auch zu M₂ gehören:
M₁ ∩ M₂:= {x| x∈ M₁ ∧ x ∈ M₂}
Man bezeichnet die Schnittmenge auch als Durchschnitt oder als Intersektion.

Wenn zwei Mengen keine gemeinsamen Elemente haben, dann ist ihre Schnittmenge die leere Menge. Die leere Menge wird durch das Zeichen symbolisiert. Zwei Mengen, deren Schnittmenge leer ist, werden disjunkt oder elementfremd genannt.

disjunkt

Zwei Mengen M₁ und M₂ sind disjunkt oder elementfremd, wenn M₁ ∩ M₂=

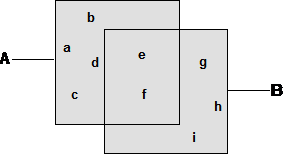
Abb. 5.4.

Die in Abb. 5.4. dargestellte Menge läßt sich beschreiben als die Menge der Elemente, die entweder zu A oder zu B oder zu beiden gehören. Man nennt sie die Vereinigungsmenge von A und B. Die Operation der Vereinigung wird durch das Zeichen ∪ symbolisiert. Für die Vereinigungsmenge von A und B schreibt man in symbolisierter Sprache

A ∪ B

Dieser Ausdruck wird gelesen als "A vereinigt mit B".

Definition 5.15. Vereinigungsmenge

Die Vereinigungsmenge zweier Mengen M₁ und M₂ ist die Menge der Elemente, die entweder zu M₁ oder zu M₂ gehören:      
M₁ ∪ M₂:={ x| x ∈ M₁ ∧ x ∈ M₂}

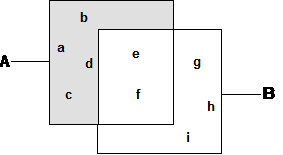
Abb. 5.5.

In Abb. 5.5. ist die Menge {a, b, c, d} hervorgehoben. Bezogen auf die Mengen A und B läßt sie sich beschreiben als die Menge der Elemente, die zu A, aber nicht zu B gehören. Sie wird Differenzmenge von A und B genannt und A − B (oder A \ B) geschrieben (lies: 'A minus B' oder 'A ohne B').

Definition 5.16. Differenzmenge

Die Differenzmenge zweier Mengen M₁ und M₂ ist die Menge der Elemente, die zu M₁ aber nicht auch zu M₂ gehören:
M₁ – M₂ := {x | x ∈ M₁ ∧ x 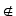M₂}

Es ist manchmal sinnvoll, den zur Diskussion stehenden Gegenstandsbereich auf eine bestimmte Menge von Individuen einzuschränken. Es macht beispielsweise keinen Sinn, von der Sterblichkeit natürlicher Zahlen zu sprechen. Wenn wir also einen Ausdruck wie 'x ist sterblich' verwenden, setzen wir stillschweigend voraus, daß 'x' zu einer Menge von Individuen gehört, denen die Eigenschaft 'sterblich' sinnvoll zugeschrieben werden kann. Man bezeichnet den einer Theorie zugrunde liegenden Individuenbereich als Grundmenge.

Definition 5.17. Grundmenge

Der Individuenbereich, über den in einem bestimmten Zusammenhang Aussagen gemacht werden, wird Grundmenge genannt (engl. universe of discourse).

Definition 5.18. Komplement

Ist A ⊆ G, so heißt G−A auch das Komplement von A bezüglich G, das auch als A geschrieben wird, wenn durch den Zusammenhang kein Zweifel besteht, welche Menge G gemeint ist, beispielsweise wenn G die Grundmenge ist.

Literatur

---