Systeme und Strukturen

Es wurde gesagt, die Linguistik sei eine Systemwissenschaft und eine Strukturwissenschaft. Im alltäglichen Gebrauch werden die Begriffe System und Struktur häufig gebraucht. Sie haben jedoch in verschiedenen Zusammenhängen teilweise verschiedene Bedeutungen. Für die Wissenschaft müssen die Begriffe System und Struktur jedoch genau definiert sein.

Im folgenden soll schrittweise auf die Definition von System und Struktur hingeführt werden.

6.1. Geordnete Paare

Wir sehen die Welt nicht als eine chaotische und gestaltlose Ansammlung von Erscheinungen, vielmehr stellen wir eine gewisse Ordnung fest, wo jedes Objekt "seinen Platz" hat und von jedem anderen Objekt unterschieden ist. Objekte können nach verschiedenen Gesichtspunkten geordnet sein, und wir selbst können Objekte nach verschiedenen Gesichtspunkten ordnen. So ordnen wir die Buchstaben, mit denen die deutsche Sprache geschrieben wird, in alphabetischer Reihenfolge, wir ordnen die Wörter in einem Lexikon nach dem Prinzip des Alphabets usw.

Ein Ordnungsprinzip ist also die Reihenfolge.

Definition 6.1. Geordnetes Paar

Wir nennen ein geordnetes Paar zwei Objekte x und y, für die eine Reihenfolge festgelegt ist, also entweder erst x und dann y oder erst y und dann x.

Geordnete Paare werden durch Spitzklammern gekennzeichnet, z.B.:

<x, y>oder  <y, x>

Geordnete Paare sind durch folgende Eigenschaft charakterisiert:

(6.1.)   <x, y> = < u, v> genau dann, wenn x = u ∧ y  = v

Daraus folgt unmittelbar:

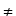(6.2.)   x y [xy ⇒ <x,y> 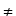 <y,x>]

Nun wird man eine Reihenfolge für irgendwelche Objekte nur dann festlegen, wenn zwischen ihnen eine bestimmte Beziehung besteht. Das legt einen Zusammenhang zwischen geordneten Paaren und Relationen nahe. So bilden z.B. Kuno und Otto ein geordnetes Paar <Kuno, Otto> hinsichtlich der Körpergröße, wenn gilt: größer(Kuno, Otto).

Genauso sinnvoll ist eine Festlegung der Reihenfolge von drei und mehr Objekten, z.B. wenn für sie drei- und mehrstellige Relationen gelten. Bei drei Elementen spricht man von einem geordneten Tripel, bei vier von einem geordneten Quadrupel und allgemein bei n von einem n-tupel:

Tripel:          < x₁, x₂,x₃>            x₁ liegt zwischen x₂ und x₃

Quadrupel:  < x₁, x₂, x₃, x₄>      x₁ kauft x₂ von x₃ für x₄

n-tupel:        < x₁, x₂, …, x_n>

Wir werden es vor allem mit geordneten Paaren zu tun haben.

6.2. Relationen und Mengen

Nun kann die Beziehung zwischen den Elementen eines geordneten Paares einfach darin bestehen, daß das erste zu einer Menge A und das zweite zu einer Menge B gehört. Nehmen wir an, die Menge A sei {Fritz, Hans, Kuno} und B {Maria, Luise}, dann ist z.B. < Fritz, Maria> ein mögliches geordnetes Paar.

Man stelle sich vor, die Herren A und die Damen B seien auf einer Tanzveranstaltung. Man kann nun z.B. fragen, wieviele Tanzpaarungen zustande kommen, wenn nur die Herren die Damen zum Tanz auffordern. Es ist die Menge aller geordneten Paare < x, y>, wobei x ein Herr, also ein Element aus A, und y eine Dame, also ein Element aus B ist. Man nennt diese Menge cartesisches Produkt von A und B (oder Verbindungsmenge ) und schreibt dafür AB (lies: A kreuz B).

Definition 6.2. Cartesisches Produkt (Verbindungsmenge) 

Seien A und B zwei (nichtleere) Mengen. Das cartesische Produkt A×B dieser Mengen ist die Menge der geordneten Paare < x, y> mit x aus A und y aus B:
AB := {<x, y> | x∈A ∧ y∈B}

In unserem Beispiel ist

AB = {<Fritz, Maria>, < Fritz, Luise>, < Hans, Maria>, < Hans, Luise>, < Kuno, Maria>, < Kuno, Luise>}

Natürlich läßt sich auch das cartesische Produkt aus mehr als zwei Mengen bilden. Sind A, B, C Mengen, dann ist ABC die Menge aller geordneten Tripel < x, y, z> mit x aus A, y aus B und z aus C. Es sei A = {der, dieser}, B = {Bursche} und C = {raucht, schläft}; dann ist ABC die Menge:

{<der, Bursche, raucht>, < dieser, Bursche, raucht>,
 <der, Bursche, schläft>, < dieser, Bursche, schläft>}

Ein Sonderfall liegt vor, wenn B = A. Das cartesische Produkt AA einer Menge A mit sich selbst ist die Menge aller geordneten Paare, die sich aus den Elementen von A bilden lassen. Man nennt diese Menge auch Paarmenge von A:

Definition 6.3. Paarmenge

Die Paarmenge AA einer Menge A ist die Menge aller geordneten Paare < x, y> mit x und y aus A: A×A :={<x, y> | x∈A ∧ y∈A}

Sei A={a,b}. Dann ist AA={<a,a>,<a,b>, <b,a>,<b,b>}

In gleicher Weise kann man von einer Tripel-Menge (AAA) und allgemein von einer n−tupel−Menge sprechen.

Konstituentenstrukturgrammatiken können auch mengentheoretisch interpretiert werden. Eine Regel wie

S → N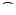PVP

wird dann aufgefaßt als

S = NPVP

d.h., die Menge der Sätze ist das kartesische Produkt aus der Menge der Nominalphrasen und der Menge der Verbalphrasen. Nominalphrasen ihrerseits sind definiert als das kartesische Produkt aus der Menge der Determinatoren und der Menge der Nomina:

NP → Det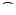N

NP=DetN

Sei Det={the, a} und N={boy, dog}, dann ist NP=DetN={<the, boy>,<the, dog>, < a,boy>, <a, dog>}

Wir haben gesehen, daß ein Allgemeinbegriff wie Pferd auf zweierlei Weise interpretiert werden kann. Es ist einmal ein Eigenschaftsbegriff, d.h. es meint die Summe der (invarianten) Eigenschaften, die jedem Exemplar 'Pferd' zukommen. Das kommt zum Ausdruck, wenn wir einen Satz wie (6.4)(a) als (6.4)(b) umschreiben:

(6.3.)   (a) Halla ist ein Pferd
(b) Halla kommt die Eigenschaft 'Pferd' zu.
(c) Pferd(Halla)

Es ist andererseits ein Klassenbegriff, d.h. es meint die Menge aller Individuen, denen die Eigenschaft Pferd zukommt. Das kommt zum Ausdruck, wenn wir (6.4)(a) wie in (6.5)(a) umschreiben:

(6.4.)   (a) Halla ist ein Exemplar aus der Menge der Pferde
(b) Halla ∈ {x | Pferd(x)}

Das gleiche gilt für alle Prädikate, auch für zwei- und mehrstellige, d.h. es gilt auch für Relationen. Die Relation größer (als) läßt sich einmal auffassen als eine Menge von Eigenschaften, die einem bestimmten Individuenpaar, z.B. Fritz und Kuno zukommt:

(6.5.)   (a) Fritz ist größer als Kuno
(b) Fritz, Kuno  kommt das Prädikat größer (als) zu
(c) größer (Fritz, Kuno)

Die Relation größer (als) läßt sich andererseits als Klassenbegriff auffassen, d.h. es bezeichnet die Menge aller Individuenpaare, denen das Prädikat größer (als) zukommt.

(6.6.)   (a) < Fritz, Kuno> ist ein Exemplar aus der Menge der Paare, zwischen denen die Beziehung größer (als) besteht.
(b) < Fritz, Kuno>∈{<x, y> | größer(x, y)}

Der Begriff Relation läßt sich wie folgt als Menge definieren:

Definition 6.4. Relation

R := {<x,y> | R(x,y)}

In diesem Sinne ist auch die Paarmenge einer Menge M eine Relation. Man nennt sie die Allrelation von M.

Definition 6.5. Allrelation

Die Allrelation einer Menge M ist gleich der Paarmenge von M.

Definition 6.6. Relation in einer Menge M

Eine Relation R ist eine Relation in einer Menge M, wenn sie in der Allrelation von M enthalten ist, d.h. wenn gilt:        
x [x∈R ⇒ x  ∈ MM]

Man wird z.B. oft die Frage stellen, zwischen welchen Elementen einer gegebenen Menge M eine bestimmte Beziehung besteht. Ein Lehrer möchte z.B. etwas über die sozialen Beziehungen zwischen den Schülern einer Klasse A wissen. Er kann z.B. fragen, welche Schüler welche anderen Schüler mögen. Gesucht ist also die Menge

{<x,y> | x∈A ∧ y∈A ∧ mag( x,y)}

Statt dessen kann man auch formulieren

(6.7.)   {<x, y> | < x, y>∈ AA ∧ mag(x, y)}

Diese Relation ist in AA enthalten, d.h. sie ist im definierten Sinne eine Relation in A.

6.3. Relationseigenschaften

Relationen können nach bestimmten Eigenschaften unterschieden werden.

Man wird z.B. sagen, daß wenn (6.10) (a) wahr ist, auch (6.10) (b) wahr sein muß, und umgekehrt:

(6.8.)   (a) Hans gleicht Peter
(b) Peter gleicht Hans

Eine Relation, die diese Eigenschaft hat, wird symmetrisch genannt.

Definition 6.7. Symmetrische Relation

Eine Relation ist symmetrisch, wenn gilt: xy  [R(x,y) ⇒ R(y, x)]

Weitere symmetrische Relationen sind: parallel (zu), gleichwertig (mit), gleichgestaltig (mit), verwandt (mit).

Ist eine Relation nicht symmetrisch, so sind zwei Fälle zu unterscheiden

1. die Relation ist nicht in allen Fällen umkehrbar, z.B. Bruder: ist a Bruder von b, dann ist b Bruder von a nur dann, wenn b männlichen Geschlechts ist;
2. die Relation ist in keinem Fall umkehrbar, z.B. größer: ist a größer b wahr, dann ist b größer a falsch; eine solche Relation heißt asymmetrisch.

Definition 6.8. Asymmetrische Relation

Eine Relation ist asymmetrisch, wenn gilt: xy [R(x, y) ⇒ ¬R(y,x)]

Wenn a größer als b ist und b größer als c, dann ist sicher auch a größer als c. Eine Relation, die diese Eigenschaft hat, wird transitiv genannt.

Definition 6.9. Transitive Relation

Eine Relation ist transitiv, wenn gilt: xyz [R(x,y) ∧ R( y, z) ⇒ R(x, z)]

Eine transitive Relation ist auch die Teilmengenbeziehung. Sind, x, y, z beliebige Mengen, so gilt:

(6.9.) xyx  [(x ⊆ y) ∧ (y ⊆ z) ⇒ ( x  ⊆ z)]

Wenn die Aussage Peter gleicht sich auch komisch klingen mag, so ist sie doch wahr. Die Aussage ist sogar für jedes beliebige konkrete Objekt wahr. Peter gleicht sich ist das gleiche wie Peter_i gleicht Peter_i. und das ist eine Aussage der Form R(x, x). Wenn für jedes Individuum x aus einem bestimmten Individuenbereich stets gilt: R(x, x), dann wird R reflexiv genannt.

Definition 6.10. Reflexive Relation

Eine Relation ist reflexiv, wenn gilt: x R(x, x)

Die Relation Teilmenge ist ein weiteres Beispiel für eine reflexive Relation. Eine Menge A ist Teilmenge einer Menge B genau dann, wenn jedes Element aus A auch Element aus B ist:

(6.10.) A ⊆ B genau dann, wenn x (x∈A ⇒ x∈B)

Nun gilt trivialerweise, x(x∈A ⇔ x∈ A) und zwar für beliebige Mengen. Folglich gilt auch: A (A⊆A).

Neben den genannten Relationseigenschaften gibt es noch eine Reihe weiterer, die hier nicht im einzelnen ausgeführt werden sollen. So gilt z.B. für die Relation Teilmenge: wenn A Teilmenge von B ist und B Teilmenge von A, dann ist A = B.

Für die Relation (leiblicher) Vater gilt: wenn a Vater von c ist und b Vater von c, dann ist a = b.

Wie die Beispiele gezeigt haben, können Relationen mehrere Eigenschaften gleichzeitig haben. So ist z.B. die Relation Teilmenge u.a. reflexiv und transitiv.

Von besonderer Wichtigkeit sind Relationen, die reflexiv, symmetrisch und transitiv sind. Sie werden Äquivalenzrelationen genannt.

Definition 6.11. Äquivalenzrelation

Eine Relation ist eine Äquivalenzrelation, wenn sie reflexiv, symmetrisch und transitiv ist.

Eine Äquivalenzrelation ist z.B. gleichgestaltig (G). Es ist leicht einzusehen, daß

• x G(x, x)     (Reflexivität)
• xy [G(x, y)⇒ G(y, x)    (Symmetrie)
• xyz [G(x, y) ∧ G(y, z) ⇒ G(x, z)]     (Transitivität)

6.4. Abbildungen

Sei R die Relation Ehemann in einem bestimmten Personenbereich P. Z.B.:

P = {Peter, Fritz, Maria, Luise, Kuno, Ina, Theodor}

R = {<Peter, Ina>, <Fritz, Luise>, < Kuno, Maria>}

Man kann nun einerseits die Menge der Elemente betrachten, die als erstes Element der geordneten Paare aus R vorkommen, also die Menge V = Peter, Fritz, Kuno. Man nennt diese Menge den Vorbereich von R. Entsprechend nennt man die Menge der Elemente, die jeweils als zweites Element der Paare aus R vorkommen, den Nachbereich von R.

Definition 6.12. Vorbereich

Der Vorbereich V einer Relation R ist die Menge der Elemente x, für die es ein Element y gibt, so daß < x, y> ein Element aus R ist:          
V(R) := {x | y < x, y>∈R}

Definition 6.13. Nachbereich

Der Nachbereich N einer Relation R ist die Menge der Elemente y, für die es ein x gibt, so daß < x, y> ein Element aus R ist:          
N(R) := {y | x < x, y>∈ R}

Eine Relation ist nacheindeutig, wenn jedem Element des Vorbereichs ein und nur ein Element des Nachbereichs zugesandte wird. Die Relation der Konfessionszugehörigkeit ist z.B. nacheindeutig, weil die Zugehörigkeit zu mehreren Konfessionen nicht zugelassen ist.

Definition 6.14. Nacheindeutig

Eine Relation ist nacheindeutig, wenn sie jedem Element des Vorbereichs genau ein Element des Nachbereichs zuordnet, d.h. wenn gilt: 
xyz  [R(x, y) ∧ R(x, z) ⇒ y=z]

Definition 6.15. Voreindeutig

Eine Relation ist voreindeutig, wenn sie jedem Element des Nachbereichs genau ein Element des Vorbereichs zuordnet, d.h. wenn gilt: 
x  y  z [R(x, z) ∧ R(y, z) ∧ x = y]

Die Relation Vater ist voreindeutig, weil jeder Mensch nur einen (leiblichen) Vater hat.

Definition 6.16. Eineindeutig

Eine Relation ist eineindeutig, wenn sie sowohl voreindeutig als auch nacheindeutig ist.

Die Relation Ehegatte ist in einer monogamen Gesellschaft eineindeutig.

Eine Relation heißt Abbildung oder Funktion,  wenn sie nacheindeutig oder kurz: eindeutig ist. Die Relation der Konfessionszugehörigkeit ist eine Abbildung.

Definition 6.17. Abbildung, Funktion 

Eine Relation ist eine Abbildung oder Funktion f, wenn sie (nach-) eindeutig ist, d.h. wenn gilt:  
x y z [R(x,y) ∧ R(x, z) ⇒ y = z]

Ist eine Relation R in der Verbindungsmenge AB enthalten, dann nennt man R eine Relation zwischen den Mengen A und B.

Beispiel: Sei A die Menge der Schüler einer bestimmten Schule und B die Menge der Lehrer dieser Schule. Dann ist die Relation R = Schüler (von) eine Relation zwischen A und B.

Definition 6.18. Abbildung aus einer Menge in eine Menge

Eine Relation R zwischen zwei Mengen A und B ist eine Abbildung aus A in B, wenn R eine Funktion ist.

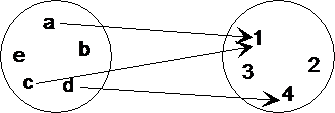
Abb. 6.6. Abbildung aus A in B

Die diesem Beispiel zugrunde liegende Funktion ist

f={<a, 1>, <c,1>,<d,4>}

Nehmen wir als weiteren Fall unser Schüler-Lehrer Beispiel. Dabei ist die Relation x hat y als Klassenlehrer eine Funktion, denn jeder Schüler hat nur einen Klassenlehrer. Diese Relation ist also eine Abbildung aus der Menge der Schüler in die Menge der Lehrer. Es liegt hier aber ein besonderer. Fall vor, denn es gibt keinen Schüler, der keinen Klassenlehrer hat. Das heißt, daß der Vorbereich der Funktion mit der Menge der Schüler identisch ist. In diesem Fall spricht man von einer Abbildung von einer Menge A in eine Menge B:

Definition 6.19. Abbildung von einer Menge in eine Menge 

Eine Relation R zwischen zwei Mengen A und B ist eine Abbildung von A in B, wenn R eine Funktion f ist und wenn gilt:
V(f) = A ∧N(f) ⊂ B

Beispiel:

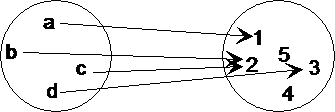
Abb. 6.7. Abbildung von A in B

Für "f ist eine Abbildung von A in B" schreibt man: f: AB.

Definition 6.20. Abbildung von einer Menge auf eine Menge

Eine Relation R zwischen zwei Mengen A und B ist eine Abbildung von A auf B, wenn R eine Funktion ist und wenn gilt:
V(f) = A ∧ N(f) = B

Beispiel:

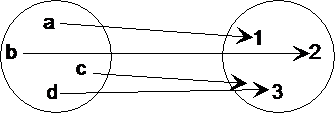
Abb. 6.8. Abbildung von A auf B

Ein Sonderfall liegt vor, wenn R eine eineindeutige Funtkion ist. Dann ist die Abbildung von A auf B selbst eindeutig.

Ist ein Paar, <x, y> ein Element einer Abbildung, so nennt man y das Bild von x und x das Urbild von y. Man schreibt

f(x) = y

für "das Bild von x ist y". Dabei ist f(x) = y nur eine andere Schreibweise für f(x, y) . Man schreibt

f^–1(y) = x

für "x ist das Urbild von y".

Eine eineindeutige Abbildung liegt dann vor, wenn jedes Urbild genau ein Bild und jedes Bild genau ein Urbild hat.

Ist A die Menge der Seiten in einem Buch und B die Menge der Seitenzahlen, dann ist R = x

hat die Seitenzahl y eine eineindeutige Abbildung von A auf B.

6.5. System und Struktur

Es ist sinnvoll, die Begriffe System und Struktur zusammen zu behandeln, weil sie sich gegenseitig bedingen. Systeme sind strukturierte Gegenstände, Strukturen sind eine Eigenschaft von Systemen, sie existieren nicht unabhängig von Systemen. Ein System ist eine "nach Ordnungsprinzipien gegliederte Mannigfaltigkeit von materiellen Dingen, Prozessen usw. (materielles System) oder von Begriffen, Aussagen usw. (ideelles System)" (Klaus/Buhr, s.v. System). In dieser Definition sind zwei zentrale mathematische Begriffe enthalten, die die Grundlage für eine allgemeine Definition des Systembegriffs bilden, nämlich die Begriffe Relation (Ordnungsprinzipien) und Menge (Mannigfaltigkeit von Dingen, Prozessen, Begriffen, Aussagen etc.). Im allgemeinsten Sinn ist ein System eine Menge von Elementen und eine Menge von Relationen zwischen den Elementen dieser Menge.

Definition 6.21. System

Ein System ist ein geordnetes Paar Σ=<M, 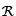>, wobei M eine Menge von Elementen ist und 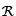eine Menge von Relationen R₁, R₂, …, R_n in M.

Ein System in diesem Sinne ist z.B. das System der natürlichen Zahlen mit M = 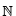 = {1, 2, 3, …} und einer Vielzahl von Relationen wie z.B.

R₁ = {<1,2>,<2,3>,<3,4>,…}

(x ist um 1 kleiner als y, f(x) = x+1)

R₂ = {<1,1>,<2,4>,<3,9>,<4,16>, …}

(f(x)=x²)

R₃={<1,1,2>,<1,2,3>,<1,3,4>, …}

(f(x,y) = x + y)

Um ein einfacheres Beispiel zu nehmen: Sei M = {Fritz, Ina, Egon, Martha, Mark} R₁= {Egon, Martha} (Ehemann)

R₂= {<Egon, Fritz>,<Egon, Ina>, < Egon, Marl>} (Vater)

R₃ = {<Martha, Fritz>, < Martha, Ina>, < Martha, Mark>}  (Mutter)

R₄ = {<Fritz, Ina>, < Fritz, Mark>, < Mark, Fritz>} (Bruder)

R₅ = {<Ina, Fritz>, < Ina, Mark>} (Schwester)

Dann ist Σ = <M, {R₁, R₂, R₃, R₄, R₅}> das Verwandtschaftssystem einer fünfköpfigen Familie.

Interessant an diesem Beispiel ist, daß nicht alle Verwandtschaftsbeziehungen explizit genannt werden müssen, weil sie aus anderen ableitbar sind. Zum Beispiel ist die Beziehung Sohn (S) aus der Beziehung Vater(V) und der Beziehung Bruder(B) ableitbar:

V(x,y) ∧ B(y,z) ⇒  S(y,x)

Aufgrund dieser allgemeinen Beziehung kann man aus R₂ und R₄ ableiten, daß Fritz und Mark Söhne von Egon sind.

Das ist wichtig für die Beschreibung von Systemen, denn man wird im allgemeinen nur die Relationen explizit nennen, die nicht aufgrund allgemeiner Gesetzmäßigkeiten von anderen Relationen ableitbar sind.

Das ist außerdem für den Strukturbegriff von Bedeutung, wenn man unter der Struktur eines Systems die Menge der Relationen in diesem System versteht:

Definition 6.22. Struktur

Ist Σ = <M, 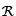> ein System, dann nennt man 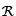die Struktur von Σ.

Der Strukturbegriff läßt sich präziser fassen über den Begriff Strukturgleichheit (Isomorphie):

Definition 6.23. Isomorphie

Zwei Systeme Σ = <M, 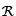> und Σ' = <M', 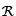'> sind isomorph (strukturgleich), wenn es eine eineindeutige Abbildung gibt, die jedem Element x aus M ein Element x' aus M' und jedem Element R_i aus 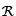ein Element R_i' aus 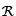' eineindeutig zuordnet, derart, daß, wenn ein n-tupel mit Elementen aus M ein Element aus R_i ist, das zugeordnete n-tupel mit Elementen aus M' ein Element aus R_i' ist.

Das klingt etwas kompliziert und soll daher gleich an Beispielen erläutert werden.

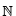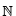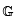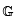Beispiel 1: Sei Σ=<, R>, wobei die Menge der natürlichen Zahlen und R die Menge der geordneten Tripeln <x, y, z> mit z = x + y ist, und Σ' = <, R'>, wobei die Menge der geraden natürlichen Zahlen und R' die Menge der geordneten Tripel < x', y', z'> mit z' = x' + y' ist. Diese beiden Systeme sind isomorph, denn es gibt eine eineindeutige Abbildung f, die jedem Element aus 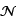genau ein Element aus 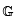zuordnet und jedem Element aus R genau ein Element aus R', wobei f(<x, y, z>) = <f(x), f(y), f(z)> ist. Für. diese Abbildung gilt f(u) = 2u. Diese Abbildung ordnet also z.B. den Elementen 2, 3, 5 aus 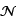die Elemente 4, 6, 10 aus 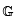zu und dem Tripel < 2, 3, 5> aus R das Tripel =4, 6, 10> aus R'. Man sieht sofort, daß 5 = 2 + 3 und 10 = 4 + 6.

Beispiel 2: Die Menge der Städte bilden mit einer Menge von Lagerelationen wie S = südlich von und W = westlich von ein System. Auf einer Landkarte sind den Städten Kartenpunkte und den Relationen S und W die Relationen U = unterhalb von bzw. L = links von eineindeutig zugeordnet. Sind zwei Städten x und y die Kartenpunkte x' und y' zugeordnet, so folgt aus S(x, y), U(x', y'). Das System der Kartenpunkte und das System der geographischen Lage von Städten sind isomorph.

Man kann nun alle Systeme, die zueinander isomorph sind, in einer Menge zusammenfassen. Die Relation der Isomorphie (I) ist reflexiv, symmetrisch und transitiv, d.h. sie ist eine Äquivalenzrelation.

Man kann die Menge zueinander isomorpher Systeme dadurch gewinnen, daß man von einem beliebigen System x ausgeht und fragt, welche Systeme zu x isomorph sind. Da die Isomorphie eine Äquivalenzrelation ist, nennt man die so gewonnene Menge eine Äquivalenzklasse.

Sei S die Menge aller Systeme, dann läßt sich die von einem beliebigen x ∈ S mit der Äquivalenzrelation I ableitbare Äquivalenzklasse wie folgt charakterisieren:

[x] = {y|y ∈ S ∧  I(x, y)}

Man nennt [x] dann die I-Äquivalenzklasse von x in S. Es ist klar, daß x selbst in dieser Klasse enthalten sein muß. Zwei solcher Äquivalenzklassen [x] und [y] sind identisch, wenn x zu y isomorph ist:

(6.11.) [x] = [y] genau dann, wenn I(x,y)

Man kann zeigen, daß die Menge der Systeme S durch die Isomorphierelation I vollständig in paarweise elementfremde Äquivalenzklassen T₁, T₂,…,T_n zerlegt wird, d.h.

S = T₁ ∪ T ₂ ∪ … ∪ T_n

T_i ∪ T_j =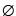 

Zwei Systeme haben die gleiche Struktur, wenn sie isomorph sind. Alle Elemente einer I−Äquivalanzklasse T_i haben die gleiche Struktur. Man kann daher sagen, daß jedes T_i einen bestimmten Strukturtyp darstellt.

Die Aufteilung in einer Menge in paarweise elementfremde Teilmengen nennt man Klassifikation.

6.6. Ordnungsstrukturen

Ordnungsstrukturen sind Strukturen, die durch sog. Ordnungsrelationen definiert werden. Ordnungsrelationen sind Relationen, die Mengen auf bestimmte Weise ordnen. Sie haben besondere Eigenschaften. Wir haben z.B. gesehen, daß der Begriff Äquivalenzrelation durch die Relationseigenschaften reflexiv, symmetrisch und transitiv definiert ist.

Betrachten wir nun als Beispiel für einen anderen Relationstyp die Relation Teilmenge. Sie wird folgendermaßen charakterisiert:

(6.12.) A  ⊆ B = x [x ∈ A ⇒  x ∈ B]

Das ist auch dann wahr, wenn man B durch A ersetzt:

(6.13.) A ⊆ A = x [x ∈ A ⇒  x ∈ A]

Daraus folgt, daß die Teilmengenbeziehung reflexiv ist.

Die Teilmengenbeziehung ist sicher nicht symmetrisch. Sie ist aber auch nicht asymmetrisch. Das ergibt sich unmittelbar aus der Reflexivität. Die Aussage A ⊆ B ⇒ B ⊆  A wird nämlich dann wahr, wenn man B durch A ersetzt: Anders ausgedrückt: wenn A in B enthalten ist und B in A, dann ist A = B.

Eine Relation, die diese Eigenschaft hat, wird antisymmetrisch genannt.

Definition 6.24. Antisymmetrisch

Eine Relation R ist antisymmetrisch wenn gilt:     
x y [R(x,y) ∧ R (y,x) ⇒  x = y]

Die Teilmengenbeziehung ist also reflexiv, antisymmetrisch und transitiv. Eine Relation, die diese Eigenschaften hat, wird Ordnungsrelation genannt:

Definition 6.25. Ordnungsrelation

Eine Relation heißt Ordnungsrelation, wenn sie reflexiv, antisymmetrisch und transitiv ist.

Ein weiteres Beispiel für eine Ordnungsrelation ist die Relation nicht größer als (= kleiner oder gleich groß) in der Menge der Zahlen. Es gilt:

1. a nicht größer als a;
2. wenn a nicht größer als b und b nicht größer als a, dann ist a = b;
3. ist a nicht größer als b und b nicht größer als c, dann ist a nicht größer als c.

Definition 6.26. Halbordnung

Ist R eine Ordnungsrelation in einer Menge M, dann nennt man R eine Halbordnung der Menge M.

An einem Beispiel soll gezeigt werden, inwiefern man von einer Ordnung sprechen kann.

Aus einer Menge A kann man eine neue Menge bilden, die aus allen Teilmengen von A besteht. Man nennt diese Menge die Potenzmenge von A:

Definition 6.27. Potenzmenge

Die Potenzmenge 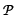einer Menge A ist die Menge aller Teilmengen von A:        
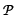(A) := {X|X ⊆ A}

Ist z.B. A = {1, 2, 3}, dann ist

(6.14.) 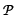(A)={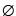, {1}, {2}, {3}, {1, 2}, {1,3}, {2, 3},{1,2,3}}

Dabei sind die Teilmengen von A aus Darstellungsgründen nach der Anzahl ihrer Elemente (nach ihrer Mächtigkeit) angeordnet. In dieser Menge ist die Teilmengenbeziehung eine Halbordnung. So gilt z.B .:

(6.15.) (a) 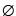 ⊆ {1} ⊆ {1,2} ⊆ {1,2,3}
(b)  ⊆ {2} ⊆ {1,2} ⊆ {1,2,3}
(c)  ⊆ {3} ⊆ {2,3} ⊆ {1,2,3}

Anschaulicher werden die Verhältnisse, wenn man die Elemente von (A) nach ihrer Mächtigkeit (ihrer Anzahl der Elemente) so in Zeilen anordnet, daß gleichmächtige Mengen in einer Zeile stehen, und dann die Mengen, zwischen denen die Teilmengenbeziehung besteht, durch eine Linie verbindet. Dabei sind die Relationspaare, die sich aus der Transitivität der Relation ergeben, gestrichelt gekennzeichnet (die Reflexivität ist nicht berücksichtigt):

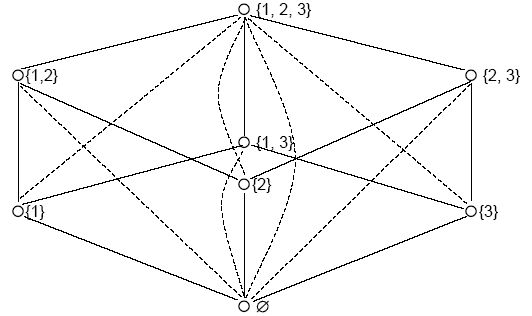
Abb. 6.9. Potenzmenge

Wie Abb. 6.9. zeigt, besteht nicht zwischen allen Elementen die Teilmengenbeziehung. So ist weder {1, 2} in {1, 3} noch {1, 3} in {1, 2} enthalten. Die Menge 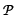(A) ist daher bezüglich der Teilmengenbeziehung nur unvollständig geordnet.

Eine Ordnungsrelation ist vollständig, wenn sie konnex ist:

Definition 6.28. Konnex

Eine Relation R ist konnex, wenn gilt:
xy [xy ⇒ R( x, y) ∨ R(y, x)]

Definition 6.29. Vollständige Ordnungsrelation

Eine Ordnungsrelation ist vollständig, wenn sie konnex ist.

Definition 6.30. Ordnung, Kette

Eine Halbordnung ist eine (vollständige oder lineare) Ordnung oder eine Kette, wenn ihre Ordnungsrelation vollständig ist.

So ist z.B. die Relation nicht größer als eine vollständige Ordnungsrelation auf der Menge der natürlichen Zahlen.

Beispiel: Sei A = {1, 2, 3, 4}

Die Ordnung von A läßt sich graphisch darstellen, indem man jedem Element aus A einen Punkt zuordnet und die einem Elementenpaar < x, y> zugeordneten Punkte mit einem Pfeil verbindet, wenn R(x, y) gilt:

 

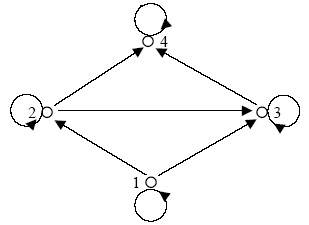
Abb. 6.10. Ordnung einer Menge

Abb. 6.10. ist die graphische Repräsentation der Ordnungsstruktur der Menge A bezüglich der Ordnungsrelation nicht größer als. Die Bezeichnungen lineare Ordnung und Kette werden einleuchtender, wenn man Abb. 6.10. vereinfacht und anders anordnet. Wir lassen die Ringpfeile weg (Kennzeichen der Reflexivität) und alle Pfeile, die Transitivität anzeigen; wir ordnen die Punkte so an, daß alle Pfeile in die gleiche Richtung weisen:

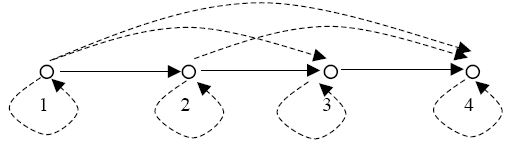
Abb. 6.11.

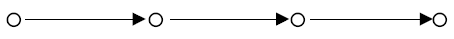
Abb. 6.12.

Nun gibt es auch Relationen, die von vornherein nicht reflexiv sondern irreflexiv sind:

Definition 6.31. Irreflexiv

Eine Relation R ist irreflexiv, wenn gilt:   
x ¬R(x,x)

Eine irreflexive Relation kann nicht antisymmetrisch sein. Sie ist entweder unsymmetrisch oder asymmetrisch.

Definition 6 .32. Strikte Ordnungsrelation 

Eine Relation ist eine strikte Ordnungsrelation, wenn sie asymmetrisch und transitiv ist.

Beispiele für strikte Ordnungsrelationen sind: größer als, kleiner als, echte Teilmenge von, Vorgänger von.

6.7. Operationen

Man kann Operationen als eine besondere Art von Relationen auffassen, wobei Elemente aus einer Menge M so miteinander verknüpft werden, daß wieder ein Element aus M entsteht. Bekannte Beispiele für Operationen sind die Addition und Multiplikation in der Menge der Zahlen. Dabei werden zwei Zahlen einer dritten zugeordnet, z.B. 1 + 2 = 3, 2·3 = 6, oder allgemein: x + y = z bzw. xy = z.

Andere Operationen sind die Verknüpfungen von Aussagen zu neuen Aussagen in der Aussagenlogik und die Verknüpfung von Mengen zu neuen Mengen in der Mengentheorie.

Die allgemeine Form einer Operation ist

(6.16.)        (x₁,…, x_n) = y

Je nachdem wieviele Elemente an der Operation beteiligt sind, müssen ein- und mehrstellige Operationen unterschieden werden. Ein Beispiel für eine einstellige Operation ist die Negation in der Aussagenlogik, die einer Aussage p die Aussage ¬p zuordnet:

Zweistellige Operationen schreibt man meist in der Form

(6.17.)        x₁x₂ = y

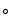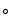Es wurde bereits gesagt, daß man Operationen als besondere Art von Relationen auffassen kann. Sei xy = z eine zweistellige Operation auf einer Menge M. Dann ordnet die Operation das Paar < x, y> einem z zu derart, daß z = xy. Man kann eine Operation daher entweder als eine zweistellige Relation R(<x, y>, z) darstellen, oder was das gleiche bedeutet — als dreistellige Relation R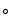(x, y, z). Allgemein ist dann eine n-stellige Operation eine zweistellige Relation mit einem n-tupel und einem weiteren Element R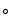(<x₁,…, x_n>,y) bzw. 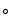eine n+1−stellige Relation R(x₁,…, x_n,y).

Die Menge aller Paare < x, y> mit x, y ∈ M ist die Paarmenge M×M. Man kann eine zweistellige Operation in M daher auch auffassen als eine Abbildung von der Menge M×M in die Menge M:

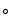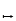f:M×MM

Allgemein ist dann eine n-stellige Operation eine Abbildung von der n-tupel-Menge Mⁿ (Mⁿ ist definiert als Mⁿ = MM^n–1) in M:

Die Struktur eines Systems, das aus einer Menge M und einer Menge O von in M definierten Operationen besteht, heißt algebraische Struktur. Ein System mit einer algebraischen Struktur kann man entsprechend algebraisches System nennen. Algebraische Systeme sind z.B. das Zahlensystem, die Aussagenlogik und die Mengentheorie.

Durch die Kombination von Ordnungsstrukturen und algebraischen Strukturen erhält man komplexe Systeme.

6.8. Literatur